목표
1. 확률의 개념
2. 베이즈 정리
3. Naive Bayes
확률
1. 확률
2. 조건부 확률
3. 조건부 독립
확률의 정의
확률 :특정한 사건이 일어날 가능성

파란 공이 뽑힐 확률: 2/3
빨간 공이 뽑힐 확률: 1/3
조건부확률
조건부 확률
어떤 사건 A가 일어 났을 때, 다른 사건 B가 발생할 확률

조건부 확률 곱셈 공식

독립
사건 A가 일어나는 것에 상관없이 사건 B가 일어날 확률이 일정할 때
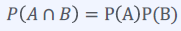
조건부 독립
사건 C가 일어났을 때 서로 다른 사건 A, B가 독립일 때

베이즈 정리
베이즈 정리의 수식

베이즈 정리 예제
속도와 결과를 나타낸 표, 마지막의 결과를 베이즈 정리로 예측해 보고자 함.











베이즈 정리 한계점과 조건부 독립


조건부 독립을 가정 - 계산량을 줄여준다

Naive Bayes 정의
Naive Bayes
- 종속 변수(Y)가 주어졌을 때 입력 변수(X)들은 모두 조건부 독립이다.
- 예측 변수들의 정확한 조건부 확률은 각 조건부 확률의 곱으로 충분히 잘 추정 할 수 있다는 단순한 가정
- 데이터셋을 순진하게 믿는다! -> Naïve(순진한) Bayes!
Naive Bayes 예시






Laplace Smoothing
Laplace Smoothing(라플라스 스무딩)
- Count하다 보면 한 번도 나오지 않는 경우도 있을 수 있다.
-> 확률이 0이 되는 것을 방지해야 함
- 최소한의 확률을 정해 준다.

Naive Bayes 장단점
장점
- 변수가 많을 때 좋다.
- 텍스트 데이터에서 큰 강점을 보인다.
단점
- 희귀한 확률이 나왔을 때 처리하기 힘들다.
- 조건부 독립이라는 가정 자체가 비현실적
'Machine Learning > 머신러닝 온라인 강의' 카테고리의 다른 글
| CH06_01. KNN (0) | 2022.10.11 |
|---|---|
| CH05_02. 스팸 메세지 분류 (Python) (0) | 2022.10.11 |
| CH04_13. 부동산 가격 예측 (Python) (0) | 2022.10.11 |
| CH04_11. 손글씨 분류 (Python) (0) | 2022.10.10 |
| CH04_10. Ensemble & Random Forest (0) | 2022.10.10 |



