목표
1. 학습 방법과 모델
2. KNN의 정의
3. 최적의 K값 설정
4. 거리의 종류
모델 학습 방법
모델 학습 방법
1. 모델 기반 학습 (Model-Based Learning)
- 데이터로부터 모델을 생성하여 분류/예측 진행
- Linear Regression, Logistic Regression

2. 사례 기반 학습 (Instance-Based Learning)
- 별도의 모델 생성 없이 인접 데이터를 분류/예측에 사용
- Lazy Learning
- 모델을 미리 만들지 않고, 새로운 데이터가 들어오면 계산을 시작
- KNN, Naive Bayes

KNN 정의
K- Nearest Neighbors
- K 개의 가까운 이웃을 찾는다.
- 학습 데이터 중 K개의 가장 가까운 사례를 사용하여 분류 및 수치 예측
KNN 분류방법
1. 새로운 데이터를 입력 받음
2. 모든 데이터들과의 거리를 계산
3. 가장 가까운 K개의 데이터를 선택
4. K개 데이터의 클래스를 확인
5. 다수의 클래스를 새로운 데이터의 클래스로 예측
KNN 분류예시
Step 0) 2개의 Class로 분류된 데이터

Step 1) 새로운 데이터를 입력 받음

Step 2) 모든 데이터들과의 거리를 계산

Step 3) 가장 가까운 K개의 데이터를 선택
예시에서는 K = 1

Step 4) K개 데이터 클래스를 확인
Class(파란색) : 0
Class(빨간색) : 1

Step 5) 다수의 클래스를 새로운 데이터의 클래스로 예측

Step 4-2) K개 데이터 클래스를 확인
K = 3 일 경우
파란색 : 2
빨간색 : 1

Step 5-2) 다수의 클래스를 새로운 데이터의 클래스로 예측

K값 설정
K- Nearest Neighbors
- K 개의 가까운 이웃을 찾는다.
- 몇 개의 K를 골라야 할까?
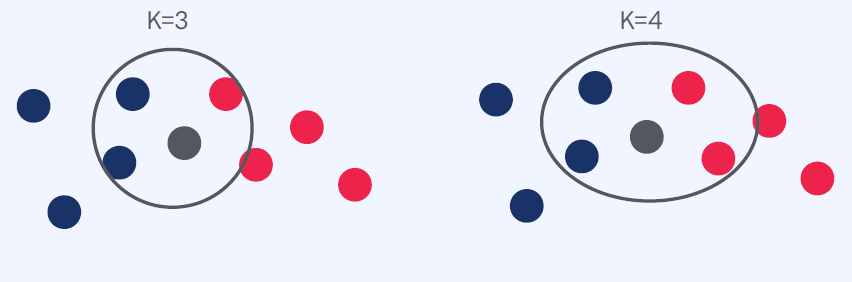
K 값에 따른 결정 경계 (Decision Boundary)

Cross Validation
- 교차 검증을 통해 제일 성능이 좋은 K 를 선택해야 한다.
- 예를 들어서 1~10 사이의 K 중 제일 성능이 좋은 K를 선택
K 는 홀수로 지정
짝수의 경우 동점이 발생할 수 있기 때문
거리의 종류
K- Nearest Neighbors
- K 개의 가까운 이웃을 찾는다.
- 가깝다를 판단할 수 있는 거리가 필요하다.
거리의 종류
1. 유클리드 거리(Euclidean Distance)
2. 맨해튼 거리(Manhattan Distance)
유클리드 거리
유클리드 거리
- 두 점 사이의 거리를 계산할 때 흔히 쓰는 방법이다.
- 두 점 사이의 최단거리를 의미한다.


맨해튼 거리
맨해튼(Manhattan) 거리
- 한 번에 한 축 방향으로 움직일 수 있을 때 두 점사이의 거리


KNN 장단점
K- Nearest Neighbors 장점
- 학습 과정이 없다.
- 결과를 이해하기 쉽다.
K- Nearest Neighbors 단점
- 데이터가 많을 수록 시간이 오래 걸린다.
- 지나치게 데이터에 의존적이다.
'Machine Learning > 머신러닝 온라인 강의' 카테고리의 다른 글
| CH06_04. 음수 가능 여부 판단 (Python) (0) | 2022.10.12 |
|---|---|
| CH06_02. KNN 실습 (Python) (0) | 2022.10.11 |
| CH05_02. 스팸 메세지 분류 (Python) (0) | 2022.10.11 |
| CH05_01. Naive Bayes (0) | 2022.10.11 |
| CH04_13. 부동산 가격 예측 (Python) (0) | 2022.10.11 |



