비용 최소화 하기 - 경사하강법 (Gradient Descent) 소개
경사하강법은
w 파라미터의 개수가 적다면 고차원 방정식으로 비용 함수가 최소가 되는 W 변숫값을 도출할 수 있겠지만, W 파라미터가
많으면 고자원 방정식을 동원하더라도 해결하기가 어렵습니다. 경사 하강법온 이려한 고자원 방정식에 대한 문제를 해결해주면서 비용 함수 RSS를 최소화하는 방법을 직관적으로 제공하는 뛰어난 방식입니다.
경사 하강법의 사전적 의미인 '점진적인 하강’이라는 뜻에서도 알수 있듯이 '점진적으로' 반복적인 계산을 통해 W파라미터값을 업데이트하면서 오류 값이 최소가 되는 W 파라미터들 구하는 방식입니다.
- 경사 하강법은 반복적으로 비용 함수의 반환 값, 즉 예측값과 실제 값의 차이가 작아지 는 방향성을 가지고 W 파라미터를 지속해서 보정해 나갑니다.
- 최초 오류 값이 100 이었다면 두 번째 오류 값은 100보다 작은 90, 세 번째는 80과 같은 방식으로 지속해서 오류를 감소시키는 방향으로 W 값을 계속 업데이트 해나갑니다.
- 그리고 오류 값이 더 이상 작아지지 않으면 그 오류 값을 최소비용으로 판단하고 그때의 W 값을 최적파라미러로 반환합니다
경사 하강법의 핵심은 " 어떻게 하면 오류가 작아지는 방향으로 W 값을 보정할 수 있을까?" 입니다
미분을 통해 비용 함수의 최소값을 찾기

어떻게 하면 오류가 작아지는 방향으로 W 값을 보정할 수 있을까?
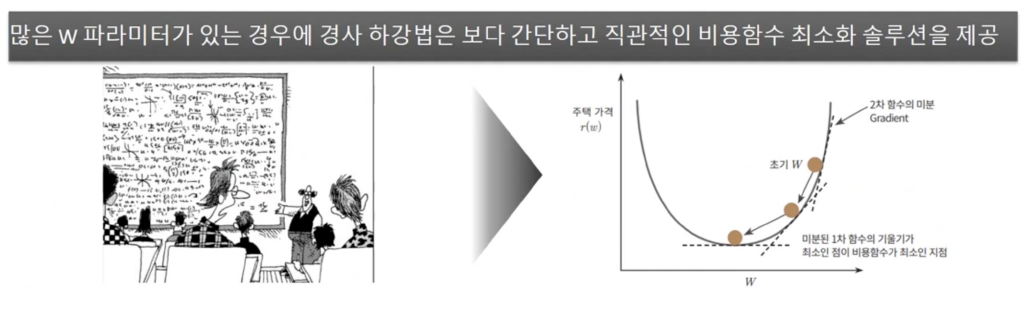
비용 함수가 다음 그림과 같은 포물선 형대의 2차 함수라면 경사 하강법은 최초 w에서부터 미분을 적용한 뒤 이 미분 값이 계속 감소하는 방향으로 순차적으로 w 를 업데이트 합니다.
마침내 더 이상 미분된 1차 함수의 기울기가 감소하지 않는 지점을 비용 함수가 최소인 지점으로 간주하고 때의 w를 반환합니다.
RSS 의 편미분
R(w) 는 변수가 w 파라 미터로 이뤄진 함수이며,

R(w) 를 미분해 미분 함수의 최솟값을 구해야 하는데, R(W) 는 두 개의 w파라미터인 w0와 w1 을 각각 가지고 있기 때문에 일반적인 미분을 적용할 수가 없고, w0, w1 각 변수에 편미분을 적용해야 합니다. R(w) 를 최소화하는 wO와 w1 의 값은 각각 r(w) 를 w0, w1 으로 순적으로 편미분을 수행해 얻을 수 있습니다.

RSS 편미분을 시작하기 전에.
편미분: 다변수 함수에 대하여 그 중 하나의 변수에 주목하고 나머지 변수의 값을 고정시켜 놓고 변수로 미분하는 일

비용함수 R(w0, w1)을 w0, w1 각각 편미분해보자

경사 하강법 정리

경사하강법 수행 프로세스

'Machine Learning > 머신러닝 완벽가이드 for Python' 카테고리의 다른 글
| ch5.3_Gradient_Descent, ch5.4_LinearModel (1) | 2022.10.12 |
|---|---|
| ch.5.4 사이킷런 LinearRegression 클래스 (보스턴주택가격예측) (0) | 2022.10.12 |
| ch.5.2 단순 선형 S회귀를 통한 회귀의 이해 (0) | 2022.10.12 |
| ch.5.1 회귀 소개 (0) | 2022.10.12 |
| 분류 (Classification) Summary (0) | 2022.10.12 |



