2 Non-Hierarchical Clustering
목표
1. 비계층적 군집화의 정의
2. K-Means
3. DBSCAN
Non-Hierarchical Clustering 정의
비계층적(Non-Hierarchical) 군집화
- 전체 데이터를 확인하고 특정한 기준으로 데이터를 동시에 구분한다
- 각 데이터들은 사전에 정의된 개수의 군집 중 하나에 속하게 된다.

Non-Hierarchical Clustering 종류
- K-Means
- DB Scan
K-Mean 정의
K-Mean의 정의
- 주어진 데이터를 K개의 군집으로 묶는 방법
K-Mean의 특징
- 각 군집은 하나의 중심을 가짐
- 각 데이터는 가장 가까운 중심에 할당
- 같은 중심에 할당된 개체들이 모여 하나의 군집을 형성
- 사전에 군집의 수, K가 정해져야 함
K-Mean 방법
K-Means 방법
1. 데이터 중 임의로 K개의 중심점(Centroid) 설정한다.
2. 모든 데이터에서 설정된 각 군집의 중심점까지의 거리 계산한다.
3. 모든 데이터를 가장 가까운 중심점이 속한 군집으로 할당한다.
4. 각 군집의 중심점을 재설정한다.
5. 군집의 중심점이 변경되지 않을 때까지 2~5를 반복한다.
Step 1) 데이터 중 임의로 K개의 중심점(Centroid) 설정한다.

Step 2) 모든 데이터에서 설정된 각 군집의 중심점까지의 거리 계산한다.

Step 3) 모든 데이터를 가장 가까운 중심점이 속한 군집으로 할당한다.

Step 4) 각 군집의 중심점을 재설정한다.

Step 5) 군집의 중심점이 변경되지 않을 때까지 반복한다.


K-Means 모수
1. 초기 중심점 설정
2. K의 개수
초기 중심점 설정
초기 중심점 설정
- K-means의 성능은 초기 중심점의 위치에 크게 좌우 된다.
- 무작위로 초기 중심 설정되는 위험을 방지하기 위한 다양한 방법이 있다.
1) 반복적으로 수행하여 가장 많이 나타나는 군집을 사용하는 방법
2) 전체 데이터 중 일부만 추출하여 계층적 군집화를 수행한 뒤 초기의 군집 중심 설정하는 방법
3) 데이터 분포의 정보를 사용하여 초기 중심 설정하는 방법
K의 개수
군집의 개수 K 설정


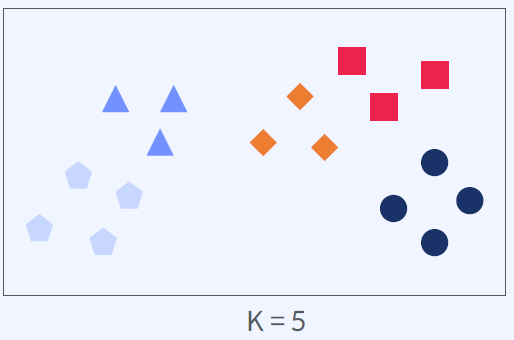
K 의 개수 SSE
SSE (Sum of Squared Error)
관측치와 중심들 사이의 거리

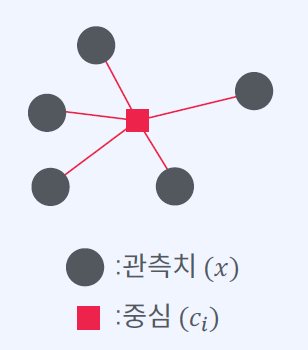
SSE 그래프
SSE (Sum of Squared Error)

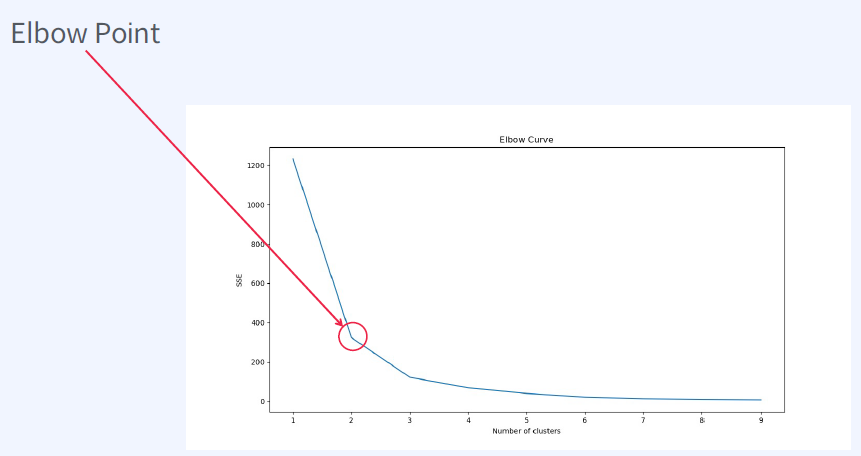
SSE 그래프 - Elbow Point
sse가 꺽이는지점, 이 지점의 k를 선택하면 된다.
K-Means 장단점
K-Means 장점
- 적용하기가 쉽다.
- 새로운 데이터에 대한 군집을 계산할 때 각 군집의 중심점과의 거리만 계산하면 되기 때문에 빠르다.
K-Means 단점
- 서로 다른 크기의 군집을 잘 못 찾음
- 서로 다른 밀도의 군집을 잘 못 찾음
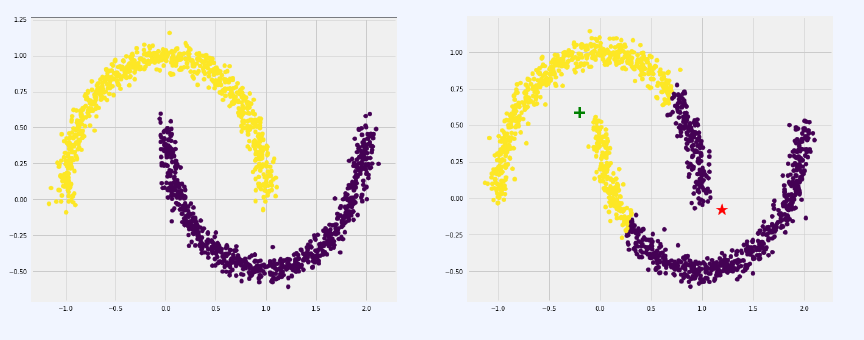
- 지역적 패턴이 존재하는 군집을 잘 못 찾음
1. 서로 다른 크기의 군집을 잘 못 찾음

2. 서로 다른 밀도의 군집을 잘 못 찾음

3. 지역적 패턴이 존재하는 군집을 잘 못 찾음
DB SCAN 정의
DB SCAN: Density-Based Spatial Clustering of Applications with Noise
점 P에서부터 거리가 e(epsilon) 내에 m(minPts)개 이상 있으면 하나의 군집으로 인식
거리가 아닌 밀도에 기반한 군집방
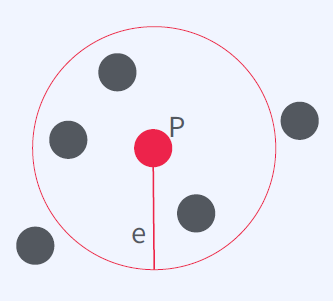
DB SCAN 방법
DB SCAN 학습 방법
1. Core Points
거리 eps이내에 데이터가 (자신 포함) minPts개 이상 있는 포인트
2. Border Points
Core Points를 이웃으로 갖고 있지만 eps 이내에 데이터가 minPts개 보다 적은 포인트
3. Noise Points
Core Points를 이웃으로 갖고 있지 않고 eps 이내에 데이터가 minPts개 보다 적은 포인트
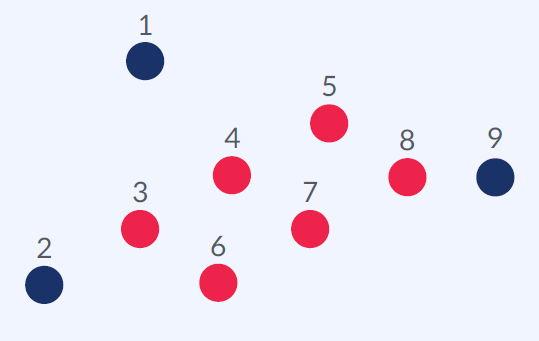
Step 1) Core Points
거리 eps이내에 데이터가 (자신 포함) minPts개 이상 있는 포인트
minPts = 4

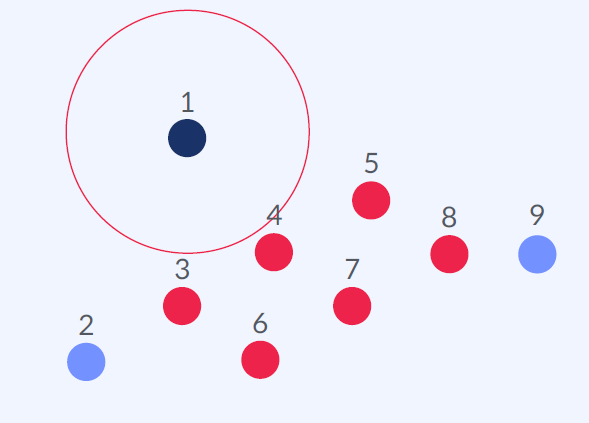
Step 2) Border Points
Core Points를 이웃으로 갖고 있지만 eps 이내에 데이터가 minPts개 보다 적은 포인트
minPts = 4


Step 3) Noise Points
Core Points를 이웃으로 갖고 있지 않고 eps 이내에 데이터가 minPts개 보다 적은 포인트
minPts = 4
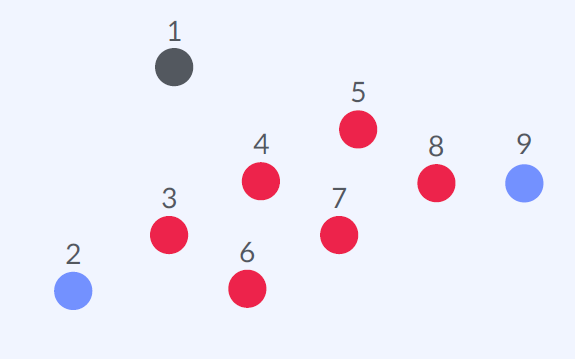
결과

DBSCAN 모수
DBSCAN 모수
1. minPts
2. eps
minPts
- 최적의 minPts를 구하는 방법에 대해서는 알려진 방법이 없다.
- Cross Validation등의 방법으로 구해야 한다.
Eps
- 주어진 minPts에 대한 최적의 거리를 구하는 방법에 대해선 K-dist Graph를 사용한다.
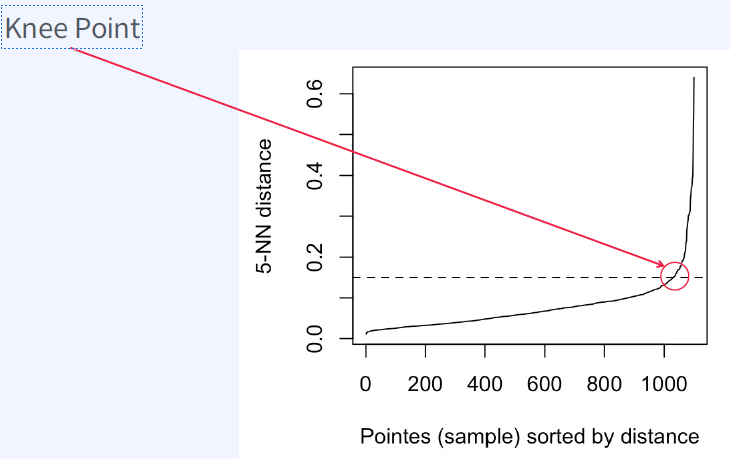
K-Dist Graph 정의
K-Dist Graph
- minPts번째 인접한 이웃 데이터 포인트까지의 거리
- 급격히 증가하기 직전의 지점(Knee Point)을 eps으로 설정한다.
DBSCAN 장단점
DBSCAN 장점
- 지역적 패턴이 있는 데이터의 군집도 찾을 수 있다.
- 노이즈 데이터를 따로 분류하여 노이즈 데이터들이 군집에 영향을 주지 않는다.
DBSCAN 단점
- 밀도가 구역에 따라 바뀔 경우를 파악하지 못한다.
Non-Hierarchical Clustering 비교
DBSCAN vs K-Means

'Machine Learning > 머신러닝 온라인 강의' 카테고리의 다른 글
| CH09_01. Dimensionality Reduction (0) | 2022.10.19 |
|---|---|
| CH08_01. Clustering (0) | 2022.10.18 |
| CH07_04. 얼굴 사진 분류(Python) (0) | 2022.10.18 |
| CH07_02. SVM 커널 실습 (Python) (0) | 2022.10.18 |
| CH07_01. SVM (0) | 2022.10.12 |



