3-2 Matrices
Matrix-Vector Multiplications
m x n 짜리 행렬과 , n개의 원소를 가지고 있는 n 차원 벡터가 있다.
여기서 행렬과 벡터의 n의 개수가 같아야 한다!
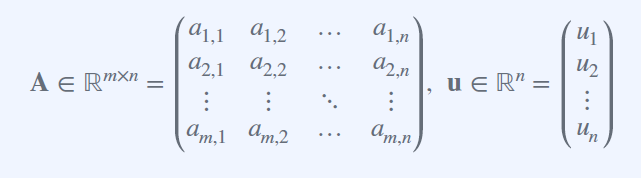
이를 곱하면 아래와 같이 된다.

고등학교 때 행렬과 벡터를 곱해주는 방식을 대학 수준으로 고상하게 표현하자면,
행렬의 각 행벡터들과 벡터를 점곱해준 것입니다.


이번엔 Columns 기준으로 Matrix-Vector Multiplications를 보자



Matrix-Matrix Multiplications
행렬 A는 m x n , 행렬 B는 n x o 이다.




A는 i번쨰 로우 ,B는 j번쨰 컬럼을 뽑는다고 생각하면된다.


'Statistics and Math' 카테고리의 다른 글
| CH04(확률)_01. 확률 (0) | 2022.09.27 |
|---|---|
| Ch03_05 역행렬 (0) | 2022.09.27 |
| CH03_03 행렬의 연산1 (0) | 2022.09.27 |
| CH03_02 벡터의 연산2 (0) | 2022.09.27 |
| CH03(선형대수)_01 벡터의 연산1 (0) | 2022.09.27 |



