3-1 Vectors 벡터의 연산2
Vector Additions
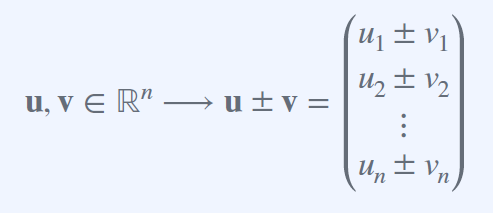
기하학적 방법에는 평행사변형, Tip to Tail 법이 있다.
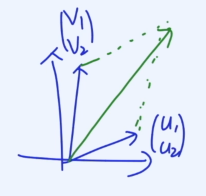
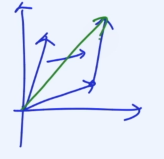
만약 스칼라 멀티플리제이션에서 -1을 넣으면, 방향이 정반대로 바뀐다.
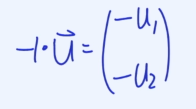
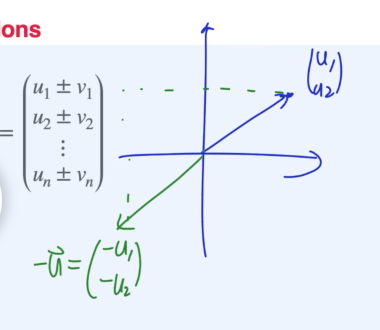
벡터의 뻴셈에 경우 아래와 같다.
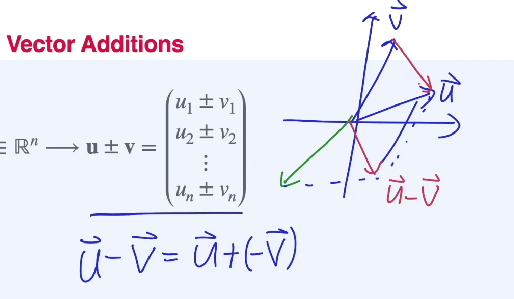
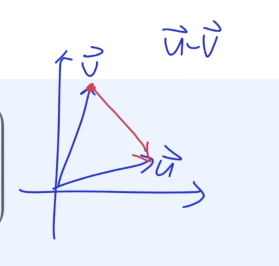
Linear Combinations of Vectors
가중평균의 합을 벡터로 구한다고 생각하면 된다.
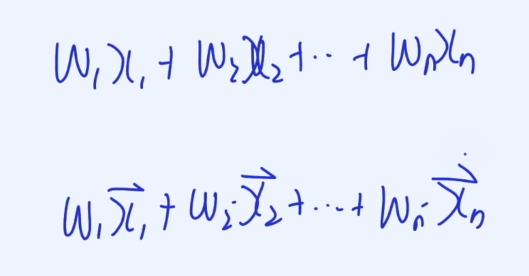
두개의 벡터에 대해서 Linear Combination과 같으면 된다.
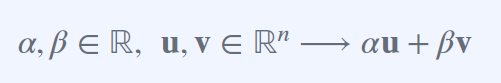

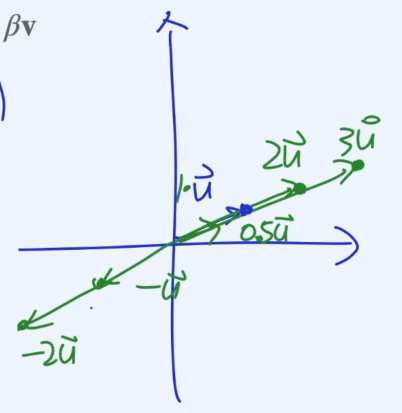
만약 알파가 임의의 실수, U가 2차원 벡터일 경우,
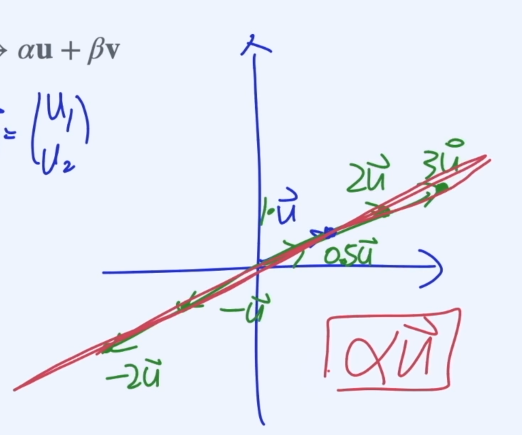
$$\alpha\vec{u}$$
는 하나의 직선으로 나타내어 진다.
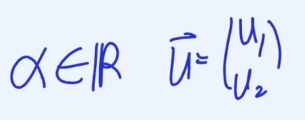
이번엔 3차원 벡터 두개에서는 Linear Combination가 가능한 모든 점들을 모으면 평면이 나온다.
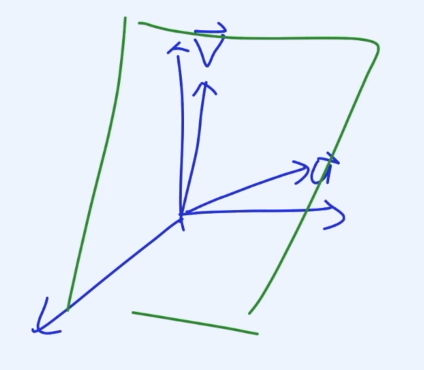
선형결합 정리
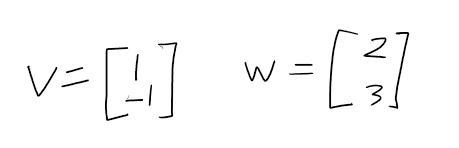
벡터에 스칼라를 곱해준 것들을 더하는 것을 바로 선형결합 또는 선형조합(linear combination)이라고 부릅니다.
벡터 v에 3을 곱한 것과 벡터 w에 2를 곱한 것을 더해주면 다음과 같이 됩니다.
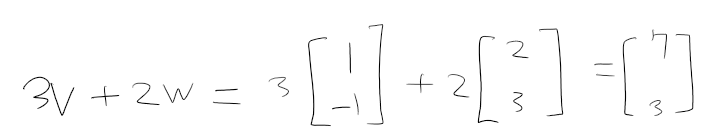
선형결합의 결과로 얻은 벡터는 다음과 같습니다. 초록색 화살표가 바로 벡터 3v + 2w입니다.
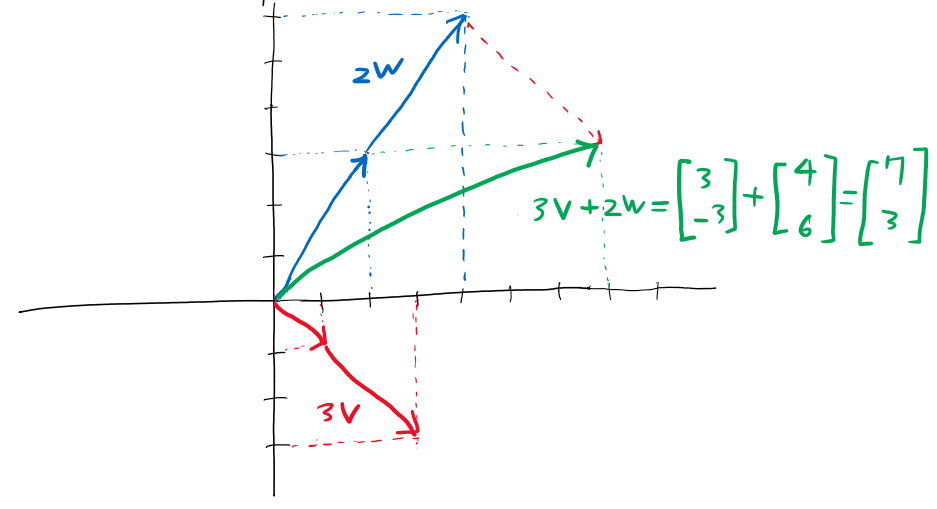
이 선형결합이라는 용어가 오늘 공부할 내용 중에서 가장 핵심이니 꼭 기억하시기 바랍니다.
지금까지는 2차원 벡터를 가지고 설명을 이어왔습니다. 그 이유는 가장 간단하기 때문입니다.
하지만 벡터는 2차원 벡터만 존재하는 것이 아니라 3차원, 4차원, 10차원,
심지어 1,000,000,000,000,000,000차원 벡터도 존재합니다.
각 벡터 당 성분의 갯수가 늘어나는 것 말고는 차이가 없습니다.
다만 4차원 이상부터는 그림을 그리기가 매우 어렵죠.
몇 차원의 벡터든 상관없이 선형결합이 가능합니다.
3차원 벡터들을 선형조합한 하나의 예는 다음과 같습니다.
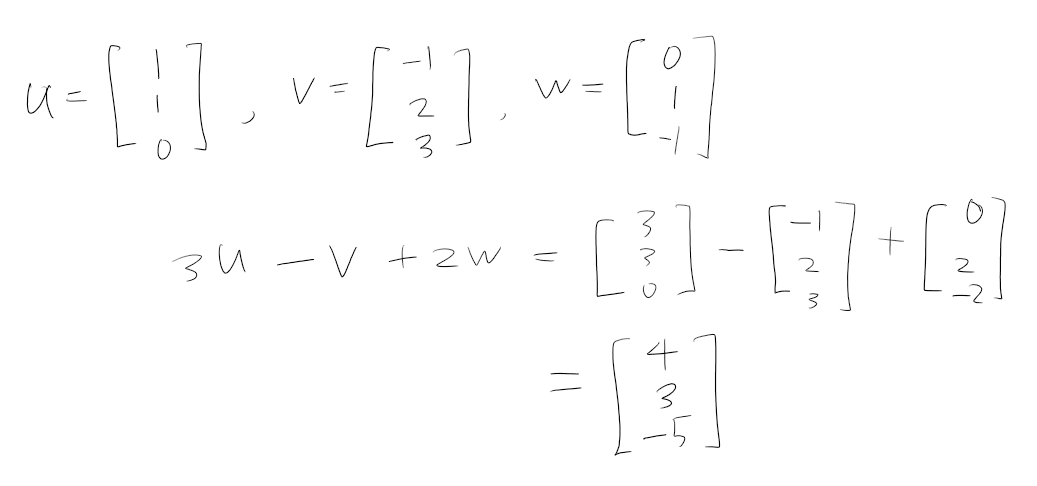
이제 정말 중요한 이야기를 할 차례입니다.
- 하나의 3차원 벡터에 스칼라를 곱해주면, 3차원 공간에서 하나의 선을 채울 수 있습니다(fill).
- 서로 방향이 다른 두 개의 3차원 벡터를 선형 결합하면, 3차원 공간에서 하나의 평면을 채울 수 있습니다.
- 서로 방향이 다른 세 개의 3차원 벡터를 선형 결합해주면, 3차원 공간 전체를 채울 수 있습니다.
이게 무슨 말인지 하나씩 이해해 가보도록 하겠습니다.
먼저 하나의 3차원 벡터에 어떤 스칼라를 곱해주더라도 하나의 직선을 떠나지 않습니다.
가능한 모든 스칼라를 곱해주더라도 결국 그 방향의 직선을 채울 뿐입니다.
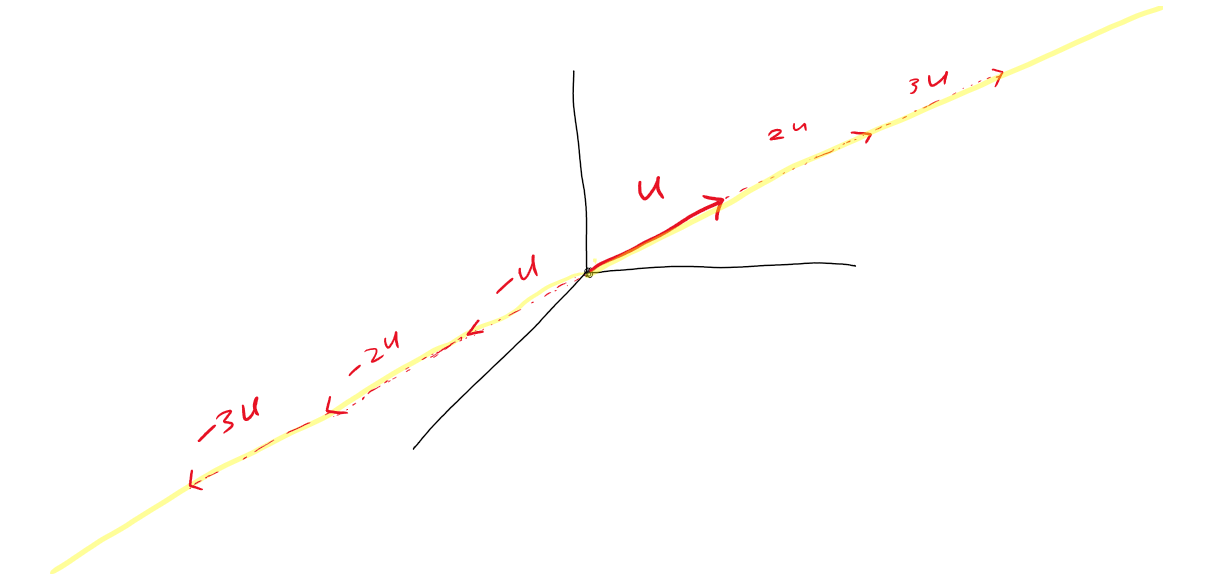
그런데 2개의 서로 방향이 다른 벡터를 선형결합한다면, 상황이 달라집니다.
모든 가능한 선형결과를 생각하면, 결국은 3차원 공간에서 하나의 평면을 채우게 됩니다.
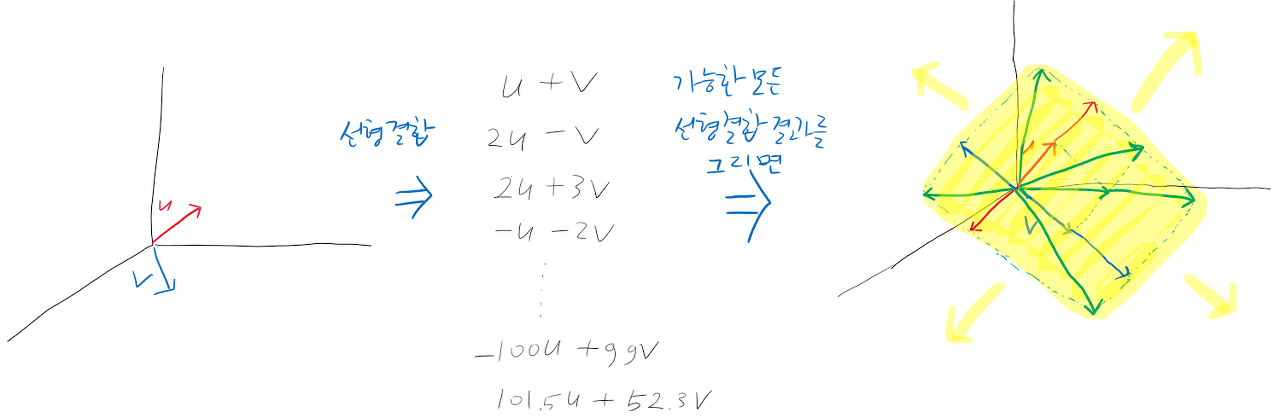
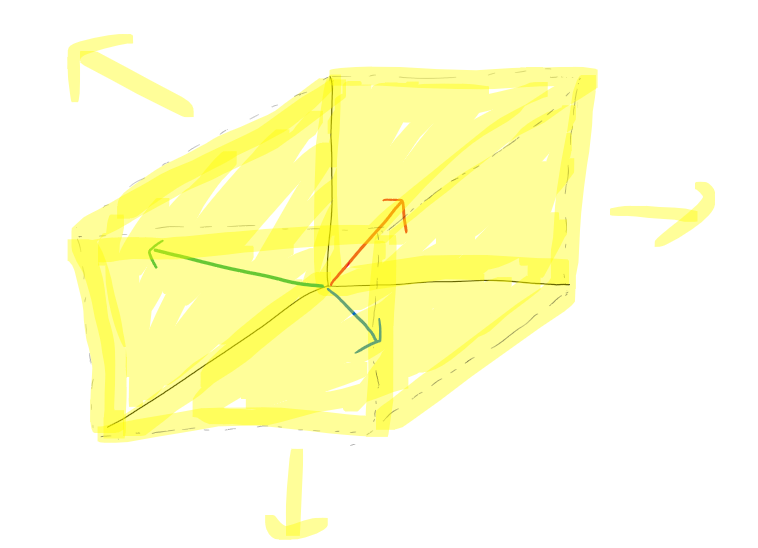
만약 서로 방향이 다른 세 개의 벡터를 선형 결합해주면 어떻게 될까요?
3차원 공간의 모든 공간을 채울 수 있게 됩니다.
그 벡터들을 선형 결합하면, 3차원 공간 내 어떤 점이라도 미칠 수 있다는 의미입니다.
어떤 점이든 u + v + w, 293.24u + 32.8v - 19.22w 등의 선형 결합으로 도달할 수 있습니다.
참고 링크
[bskyvision의 선형대수학, 제1강] 벡터와 선형결합
지난 강의: [bskyvision의 선형대수학, 제0강] 동기부여: 선형대수학 F 받았던 학생이 선형대수학을 이용해서 SCI 논문을 쓰다 자, 이제 그러면 본격적으로 선형대수학 공부를 함께 시작해봅시다. 제0
bskyvision.com
Dot Products
점곱(dot product)
점곱은 내적(inner product)이라고도 부릅니다. 아마 내적이란 단어가 좀 더 익숙한 분들이 많으실 것입니다.
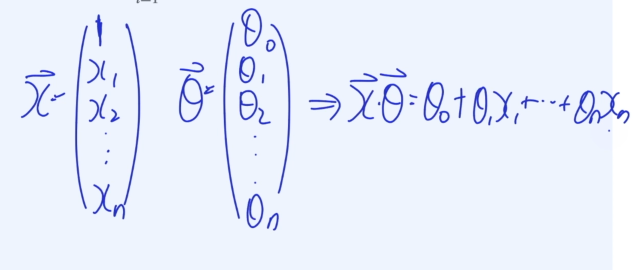
두 벡터의 점곱은 다음과 같이 정의됩니다. 점곱은 같은 위치의 성분끼리 곱해준 것들을 모두 더하는 것입니다.
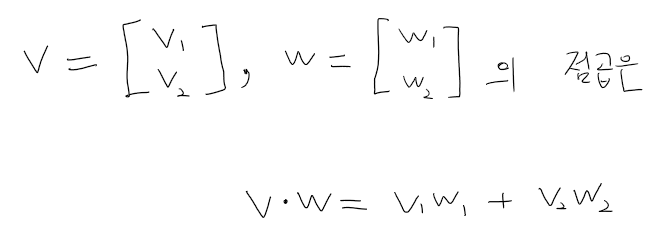
만약 v와 w가 다음과 같다면, 두 벡터의 점곱은 이렇게 계산됩니다.
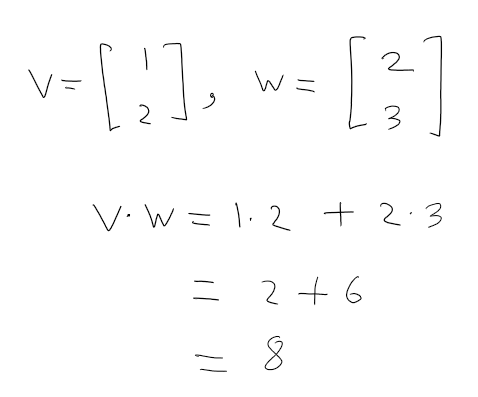
보시다시피 점곱의 결과는 벡터가 아닌 하나의 숫자로 나타나게 됩니다.
3, 4, 5, 100차원의 벡터들의 점곱도 마찬가지로 동일한 방식으로 구하면 됩니다.
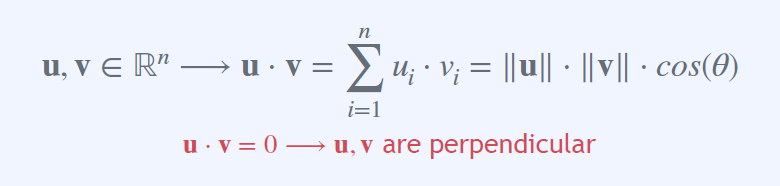
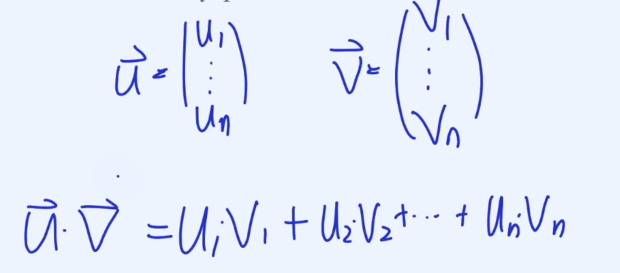
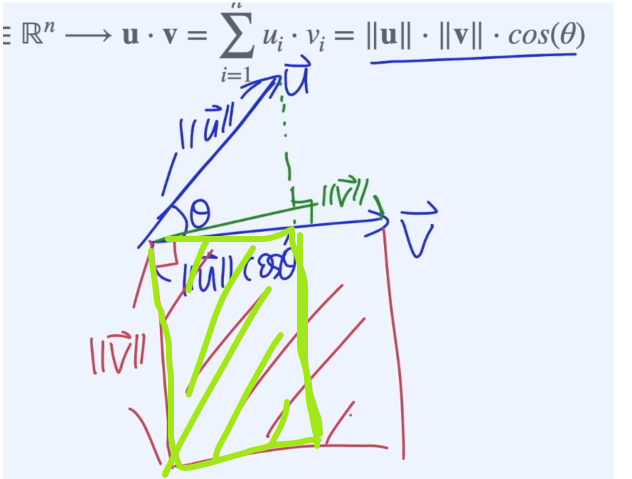
기하학적으로 Dot Product를 보면 아래와 같다.
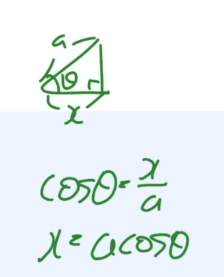
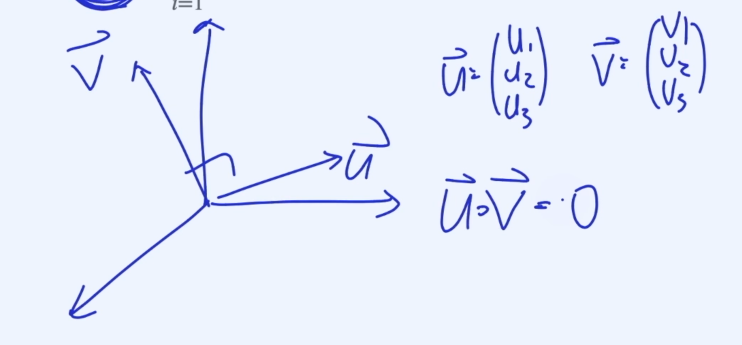
점곱의 결과가 0이라면?
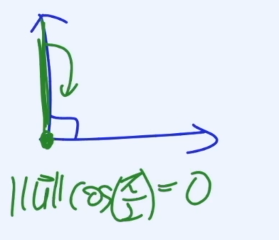
만약 점곱의 결과가 0이 된다면, 이때는 상당히 중요한 기하하적(geometrical) 의미를 갖습니다.
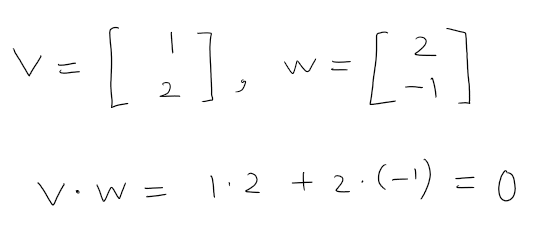
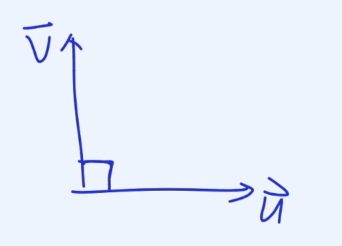
어떤 기하학적 의미를 갖고 있는지 파악하기 위해 이 두 벡터를 그려보겠습니다.
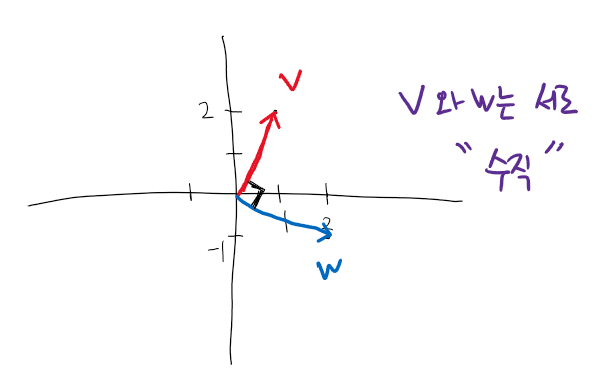
서로 수직(perpendicular) 관계에 있죠? 그렇습니다.
점곱이 0이라면, 두 벡터는 서로 수직 관계를 갖습니다. 상당히 중요한 내용이니 꼭 기억하고 넘어가세요.
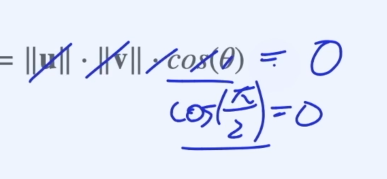
'Statistics and Math' 카테고리의 다른 글
| CH03_04 행렬의 연산2 (0) | 2022.09.27 |
|---|---|
| CH03_03 행렬의 연산1 (0) | 2022.09.27 |
| CH03(선형대수)_01 벡터의 연산1 (0) | 2022.09.27 |
| CH01_10. 선형함수 (0) | 2022.09.27 |
| CH01_09 함수의 변형 (0) | 2022.09.27 |



