3-1 Vectors 벡터의 연산
Vectors
벡터란 무엇인가?
여기에는
- 물리적 관점 : 크기와 방향으로 정의되는 값이며, 크기와 방향이 같다면 어디에 존재하든 같은 벡터이다.
- 컴퓨터과학적 관점 : 순서가 존재하는 숫자의 리스트(list) , 순서가 같지 않으면 같은 벡터가 아님
- 수학적 관점 : " 두 벡터의 합 / 벡터와 숫자의 곱 " 두가지 개념(operation) 을 잘 만족할 수 있다면 무엇이든 될 수 있다.



https://iagreebut.tistory.com/53 (참조 링크)
벡터(vector)란?
그래픽스에 선형대수가 많이 사용된다고 하셔서 .. 이미 수강했지만 정말 다까먹었으므로 좋은 유튜브 강의를 보면서 다시 공부하고 기억을 다시 떠올리는 의도로 벡터란 무엇인가? 여기에는
iagreebut.tistory.com
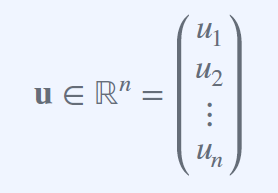
집합 같은 경우 순서가 중요 하지 않으며, 중복도 허용되지 않는다.
하지만 벡터는 순서가 중요하며, 중복도 허용된다.
Row / Column Vectors

좌표 평면상에 한점을 벡터로 표현하면 아래와 같다.


Transposes of Vectors (백터의 전치)


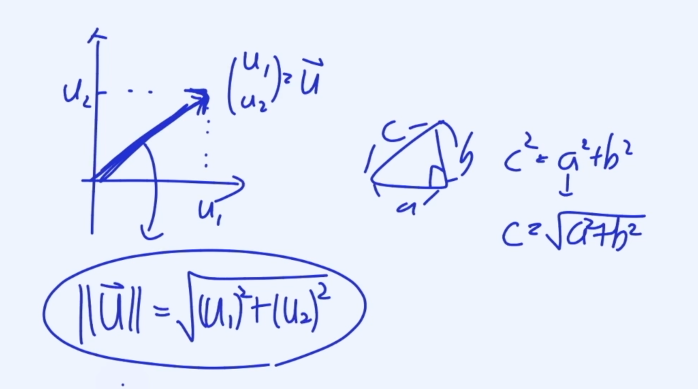
Vector Norms(L2 Norms)
벡터의 노움은 화살표의 길이
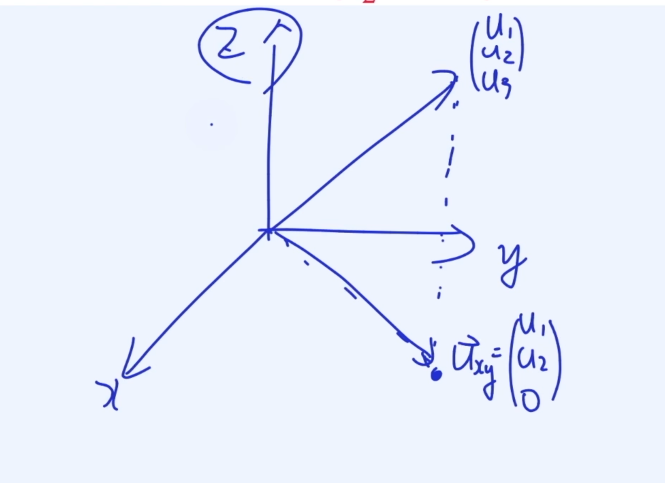
3차원 좌표 평면에서 놈을 구해보자
우선 U1,U2,U3 점애서 Z좌표가 0인점을 찍고,
이를 이용하여 원점에서 그 좌표까지의 거리를 구한다.
그리고 그 직선과 원래의 좌표와 원점을 삼각형으로 보고
피타고라스 정리에 의해서 U1,U2,U3의 노움을 구하면 아래와 같이 된다.
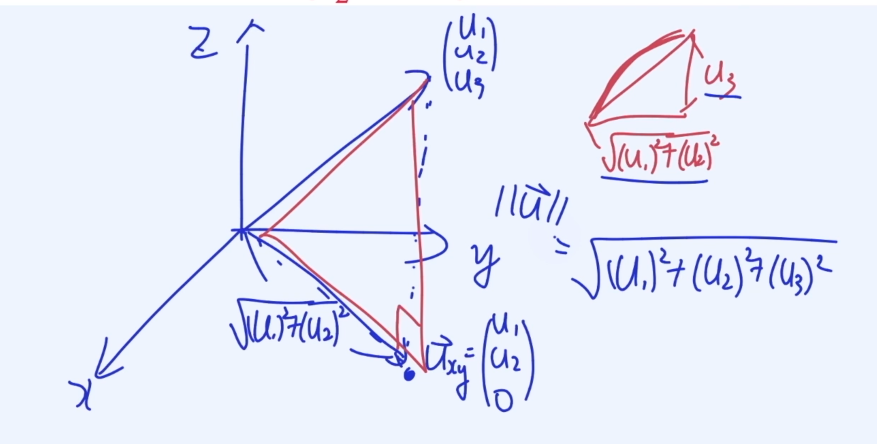
이것을 L2 Norm 이라고 부른다.
이를 유클리디안 노움이라고 부른다.
다차원의 노움의 공식은 아래와 같다.
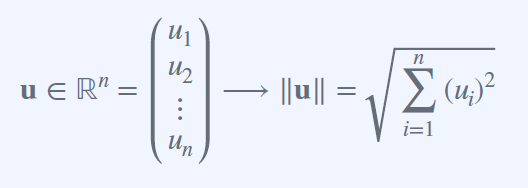
Scalar Multiplications of Vectors
Note! if α < 0, then the direction is reversed

Vector Unitizations
Unit Vectors
놈 자체가 1인 벡터
∥u∥ = 1⟶ u is an unit vector
Vector Unitizations
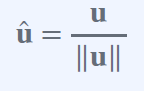
유닛 벡터로 만들기 위해선
놈을 U벡터에 나눠주면 된다.
놈 자체는 스칼라 값이다. 따라서 스칼라 값을 벡터에 곱하는
Scalar Multiplications 이 된다.

위의 유닛 벡터의 놈을 구하면 1이 됨을 볼 수 있다.

'Statistics and Math' 카테고리의 다른 글
| CH03_03 행렬의 연산1 (0) | 2022.09.27 |
|---|---|
| CH03_02 벡터의 연산2 (0) | 2022.09.27 |
| CH01_10. 선형함수 (0) | 2022.09.27 |
| CH01_09 함수의 변형 (0) | 2022.09.27 |
| CH01_08 초월함수 (0) | 2022.09.27 |



