PCA(Principal Component Analysis) 의 이해
• 고 차원의 원본 데이터를 저 차원의 부분 공간으로 투영하여 데이터를 축소하는 기법
• 예를 들어 10차원의 데이터룰 2자원의 부분공간으로투영하여 데이터를축소
• PCA는 원본데이터가 가지는 데이터 변동성을 가장 증요한 정보로 간주하며 이 변동성에
기반한 원본 데이터 투영으로 차원 축소를 수행

PCA는 제일 먼저 원본 데이터에 가장 큰 데이터 변동성 (Variance) 을 기반으로 젓 번째 벡터 축을 생성하고, 두 번째 측은 젓번째 축을 제외하고 다음으로 변동성이 큰 축을 설정하는 데 이는 젓번째 축에 직각이 되는 벡터(직교 벡터)측 입니다. 세 번째 축은 다시 두번째 축과 직각이 되는 벡터를 설정하는 방식으로 축을 생성합니다. 이렇게 생성된 벡터 축에 원본 데이터를 투영하면 벡터 축의 개수만큼의 자원으로 원본 데이터가 자원 측소됩니다.
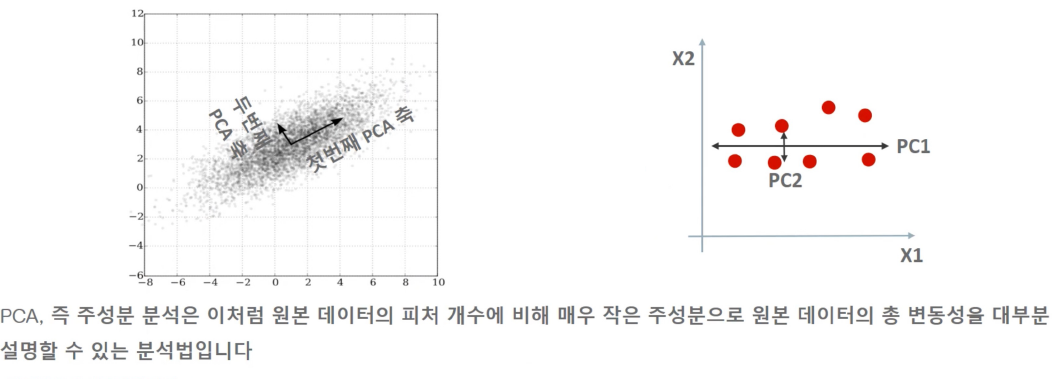
PCA 변환
PCA를 선형대수 관점에서 해석해 보면 , 입력 데이터의 공분산 행렬 ( Covariance Matrix) 을 고유값 분해하고 ,이렇게 구한 고유벡터에 입력 데이터를 선형 변환하는 것입니다.

공분산 행렬
보통 분산은 한개의 특정한 변수의 데이터 변동을 의미하나, 공분산은 두 변수간의 변동을 의미합니다. 즉,사람 키 변수를 x, 몸무게 변수를 Y 라고 하면 공분산 Cov(X, Y) > 0은 X( 키)가 증가할 때 Y( 몸무게)도 증가한다는 의미입니다.

선형 변환과 고유 벡터/고유값

공분산 행렬의 고유값 분해

PCA 변환과 수행 절차

PCA를 이용한 데이터 차원 축소실습
사이킷런 PCA

'Machine Learning > 머신러닝 완벽가이드 for Python' 카테고리의 다른 글
| Recommation System ch1. 추천시스템이란? (0) | 2022.10.20 |
|---|---|
| ch6.4 SVD(Singular Value Decomposition) (0) | 2022.10.20 |
| ch6. 차원 축소 (0) | 2022.10.20 |
| 예제 1-2. bike-sharing-demand_랜덤포레스트회귀 (0) | 2022.10.13 |
| 예제 1-1. bike-sharing-demand_EDA (0) | 2022.10.13 |



