1-2 Sets, 집합의 포함관계
Inclusion and Exclusion (포함과 배제)

삼지창 모양, 원소와 집합사이의 포함관계
Equal Sets

집합 A의 모든 원소가 집합 B에 포함이 된다.
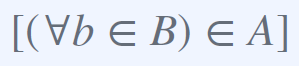
집합 B의 모든 원소가 집합 A에 포함이 된다.
이를 밴다이어 그램으로 표현하면 아래와 같다.
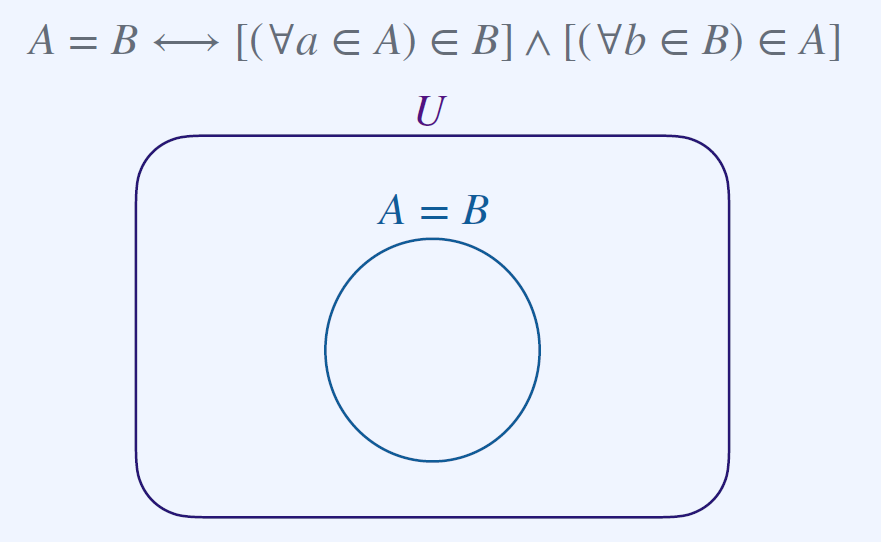
Subsets and Supersets
Subsets
집합 A의 모든 원소가 집합 B에 포함될 때, A는 B의 subset이라 한다.
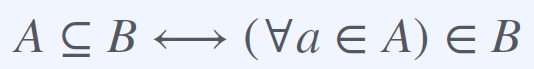

또한 subset인 A의 원소의 개수는 B의 원소의 개수보다 작거나 같을 것이다.

Supersets
집합 B의 모든 원소가 집합 A에 포함될 때, A는 B의 superset이라 한다.

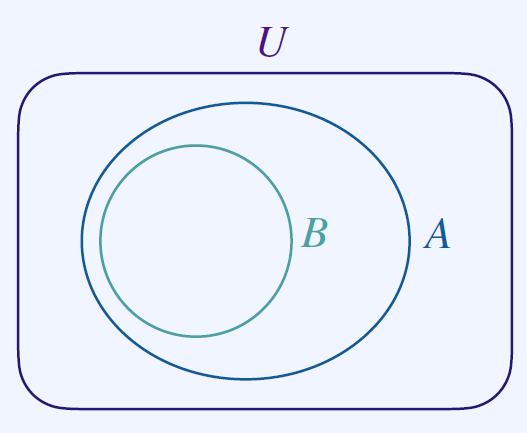
또한 Supersets인 A의 원소의 개수는 B의 원소의 개수보다 작거나 같을 것이다.

Proper Subsets
집합 A, B에 대해 A가 B의 subset이지만 완전히 같지는 않을 때, A는 B의 proper subset이라 한다.
적어도 B의 원소 중 하나는 A에 포함되지 않아야 한다.
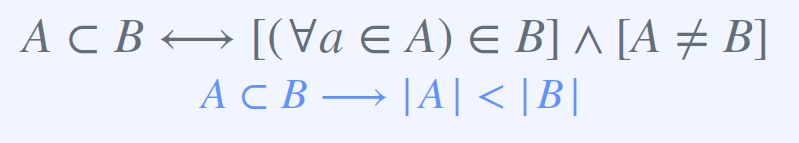
Proper Supersets
집합 A, B에 대해 A가 B의 superset이지만 완전히 같지는 않을 때, A는 B의 proper superset이라 한다.
적어도 A의 원소 중 하나는 B에 포함되지 않아야 한다.

cf) 참조
$$ \exists 는\ 존재한다라는\ 수학 \ 연산자이다\\따라서 \ 위의 \ Proper Subset의\ 산식을 \ 존재연산자를 \ 사용하여 \ 표시할 수 있다.$$
$$ \left [ (\forall a\in A)\in B \right ]\wedge \left [ (\exists b\in B)\notin A \right ]\\ A의 \ 모든 \ 원소는 \ B에 \ 포함되면서, \ 적어도 \ B에서 \ 존재하는 \ 원소 \ 하나는 \ A에 \ 포함되지 \ 않는다. $$
'Statistics and Math' 카테고리의 다른 글
| CH01_05. 파티션 (0) | 2022.09.26 |
|---|---|
| CH01_04 집합의 연산 (1) | 2022.09.26 |
| CH01_02 집합 (2) | 2022.09.26 |
| CH01_01 .대수학적 특징과 항등원, 역원 (2) | 2022.09.26 |
| 단순 회귀 분석 (0) | 2022.08.18 |



