4-5 Random Distributions
Probability Mass / Density Functions

주사위를 돌렸을 떄 확률변수와 확률을 표현한 표를 보자
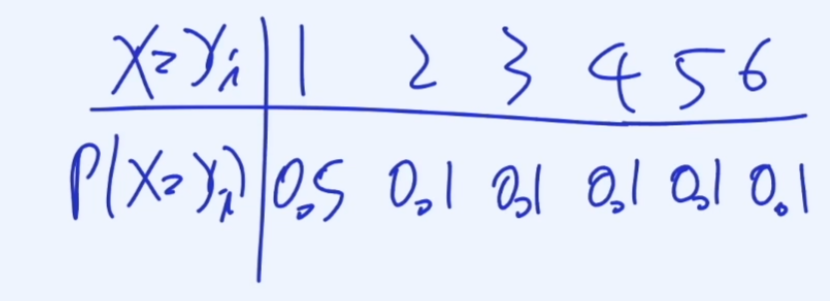
확률과 확률변수와의 관계를 그래프로 나타내면 아래와 같다.

이러한 양상은 이산 분포를 보인다.
이산 확률 분포의 경우 이와 같은 그래프를 보인다.
반연 연속 확률 분포에 대해서 보자

만약 키가 170이 될 확률은 얼마일까
키가 170일 확률은 0에 가깝다
왜냐하면 키가 완전히 정확하게 170일 경우는 거의 없을거기 때문이다.

반면 범위를 설정해서 확률을 구할 수 도 있다
키가 170~170.1 일일 확률을 표시하면 아래와 같다.

따라서 이러한 확률을 구하기 위해서는 적분을 통하여 구해야 한다.

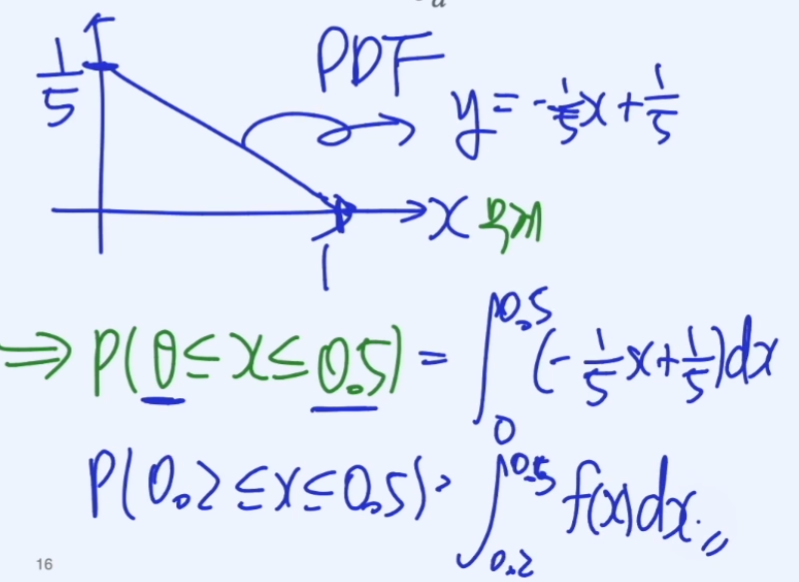
이처럼 연속적인 확률분포를 표현한 것을 연속 밀도 함수이다.
Binomial Distributions (이항 분포)
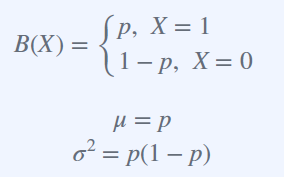
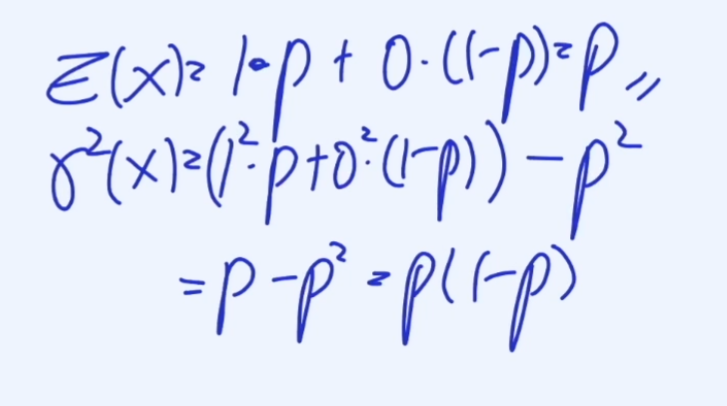
확률 질량 함수(Probability Mass Functions) 의 대표적인 함수.
동전던지기 처럼 두가지 상황에 대한 확률이 존재하는 경우에 해당된다.
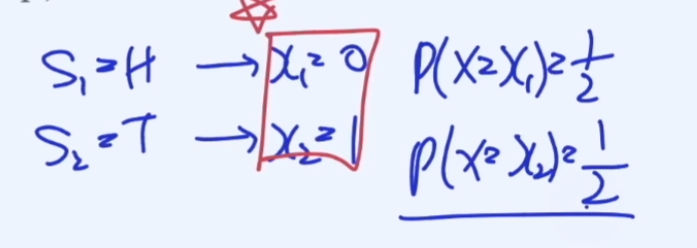

만약 동전을 망치로 쳐서 확률이 변경된 경우에는 아래와 같다.
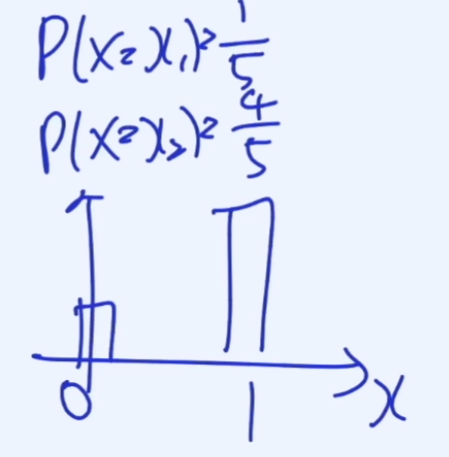
Normal Distributions (정규분포)

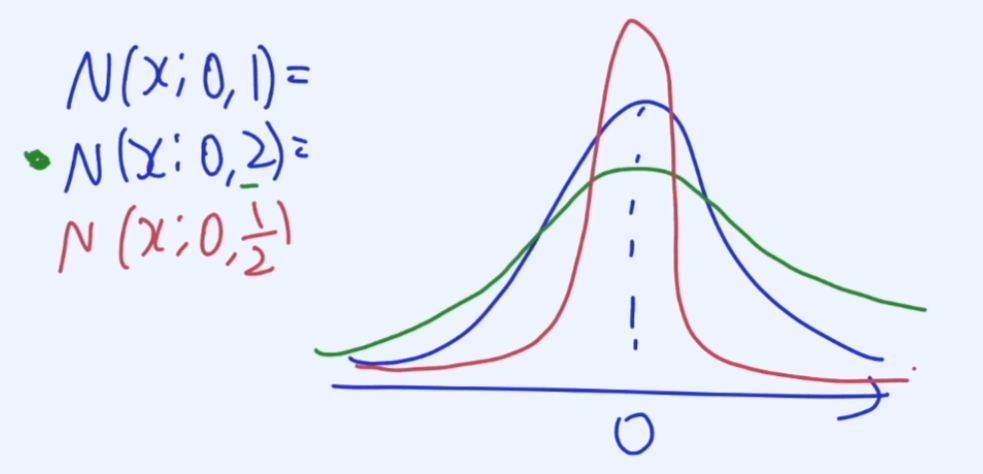
68-95-99.7 Rules
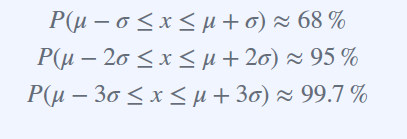
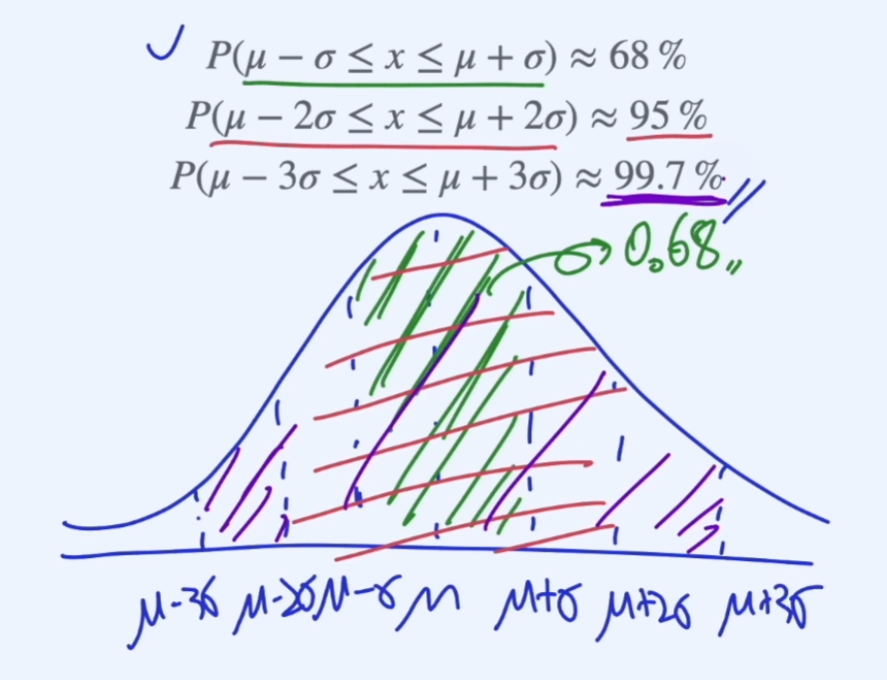
정규 분포의 Outlier는 99.7%, 3 시그마에 해당되지 않는 경우를 말한다.
'Statistics and Math' 카테고리의 다른 글
| 미분학(강의) (1) | 2022.09.29 |
|---|---|
| CH04_08 시그모이드와 소프트맥스 (0) | 2022.09.28 |
| CH04_06 확률변수의 기댓값과 산포도 (0) | 2022.09.28 |
| CH04_05 확률변수 (0) | 2022.09.28 |
| 선형대수학(강의) (0) | 2022.09.28 |



