4-4 Expectations and Variances
Expected Values

주사위를 던지는 경우의 예시를 생각해보자.

이에 대한 기대값을 구해보자.

로또의 경우를 생각해보자.
꽝, 2등, 1등을 상금이라는 확률변수로 표현해보자.

이러한 확률변수와 확률의 표를 가정하면 아래와 같다.


이러한 기대값이 나온다. 물론 기대값이 2천만원이라는 비정상(?)적인 값이 나왔다
매우 좋은 로또인 것을 볼 수 있다.
따라서 좀더 확률을 낮춰보자.

이때의 기댓값을 구해보자.

따라서 기댓값이 약 만원임을 알 수 있다.
만약 로또의 가격이 12000원 이였으면 사면 안되는 복권으로 볼 수 있다.
Expectations of a Function

아래와 같이 기댓값 있는 확률변수 x가 있을때, 그러한 확률변수를 넣을 수 있는 함수 g(x)가 있다고 가정하자.
g(x) = x^2일때, 그 값은 아래의 표와 같다.
이러한 상황에서 확률변수 x와 함수 g(x)는 같은 확률을 가지고 있다.
또한 함수 g(x)를 확률변수 Y라는 새로운 확률변수로 볼 수 있다.


새로운 함수 h를 Log함수로 보고 또한 Z라는 확률변수로 가정하자.
이러한 확률변수 Z의 기댓값은 아래와 같다.


Variances

제평평제 = 제곱의 평균 - 평균의 제곱 (고등학교때 외욌던거)
(X - 평균)을 새로운 확률변수 Y라고 두면 아래와 같은 식이 나온다.

이에 대한 기댓값을 구하면 아래와 같다.

이럴떄 이 값은 의미하는 바는 무엇일까

이럴떄 평균(기댓값)에서 부터 얼마나 떨어져 있는지 나타낸 것이라고 볼 수 있다.
Standard Deviations
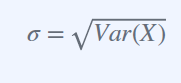
표준편차는 분산에 루트를 씌운 값이다.
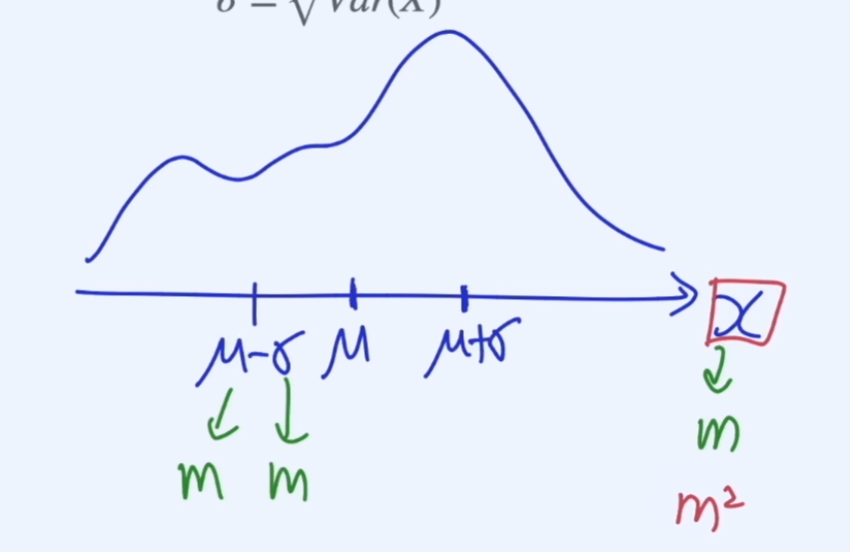
분산은 값이 높아서, 루트를 씌워서 표준편차를 통해 그래프에서 표현할 수 있다
따라서 표준편차는 확률변수와 같은 단위로 표현하기 위해 사용한다.
.
'Statistics and Math' 카테고리의 다른 글
| CH04_08 시그모이드와 소프트맥스 (0) | 2022.09.28 |
|---|---|
| CH04_07 이산, 연속 확률분포 (0) | 2022.09.28 |
| CH04_05 확률변수 (0) | 2022.09.28 |
| 선형대수학(강의) (0) | 2022.09.28 |
| Ch04_04 베이즈 정리 (0) | 2022.09.27 |



