4-6 Sigmoid and Softmax
Logits
Logit은 확률을 다르게 표현 한 것.
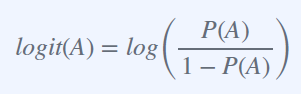
odds를 아래와 같이 부른다.


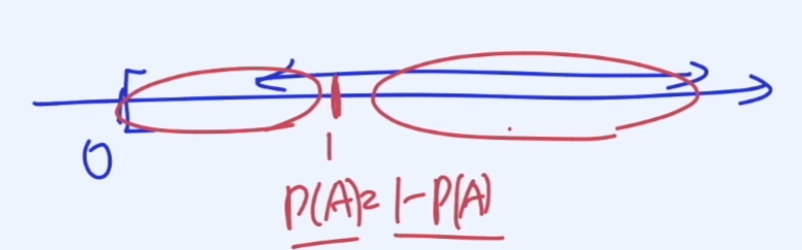
만약 P(A) = 1/2 일 경우
Odds는 1값이 나온다.
이때 P(A) = 1 - P(A) 가 성립한다.

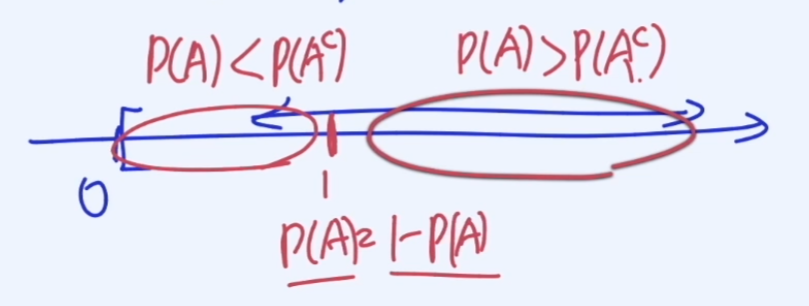
양쪽이 비대칭이므로 로그를 취한다.



로그를 취해서 그래프를 그리면 대칭적인 그래프를 보여준다.
Sigmoid and Logits
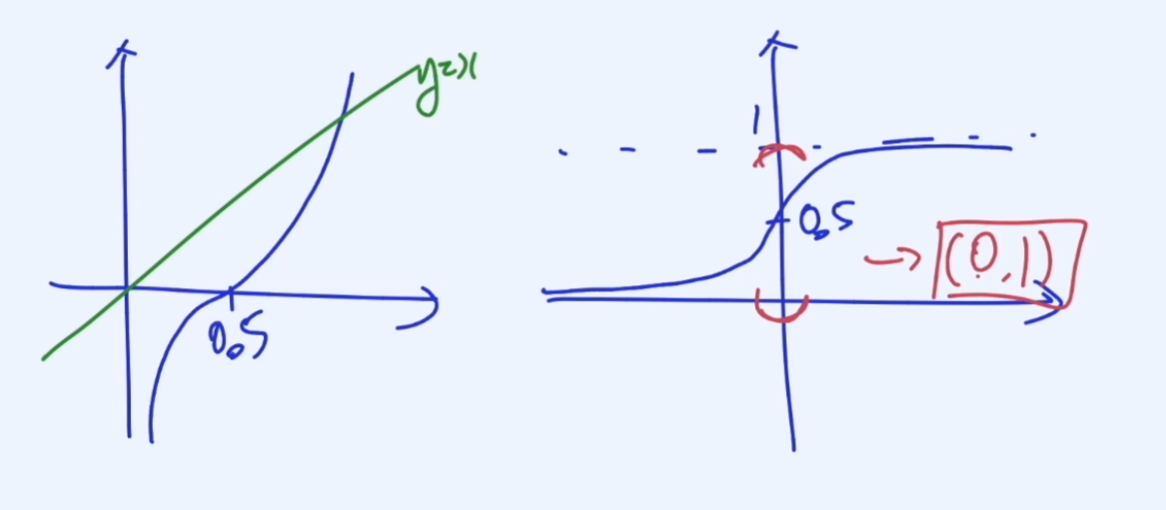
logits의 역함수를 구해보자.
그러면 Sigmoid 함수가 나온다.
따라서 logits의 역함수가 sigmoid임을 알 수 있다.


확률에 log를 씌운것이 logits 그것의 역함수가 sigmoid이다.
이때 sigmoid는 그것을 다시 확률로 표현된다.
이때 sigmoid의 확률이 0과 1로 표시된다.
반면에 logit의 범위는 무한대이다.
따라서 sigmoid로 확률을 표현할 수 있다;

Probability Vector and Softmax
sigmoid를 일반화 시킨것이 Softmax이다.

logits 벡터를 Softmax에 넣으면 sigmoid 벡터로 확률 벡터로 표현된다.
'Statistics and Math' 카테고리의 다른 글
| 통계(강의) (1) | 2022.09.29 |
|---|---|
| 미분학(강의) (1) | 2022.09.29 |
| CH04_07 이산, 연속 확률분포 (0) | 2022.09.28 |
| CH04_06 확률변수의 기댓값과 산포도 (0) | 2022.09.28 |
| CH04_05 확률변수 (0) | 2022.09.28 |



