4-3 Random Variables
Random Variables
확률변수는 Function의 개념이다.
Outcome인 s를 실수인 x에 대응하는 개념

주사위를 굴릴 때, 이미 Outcome들은 실수로 나타나져 있다.
그러나 동전 던지기 경우 Outcome은 앞면, 뒷면 처럼 실수로 나타내지지 않는다.
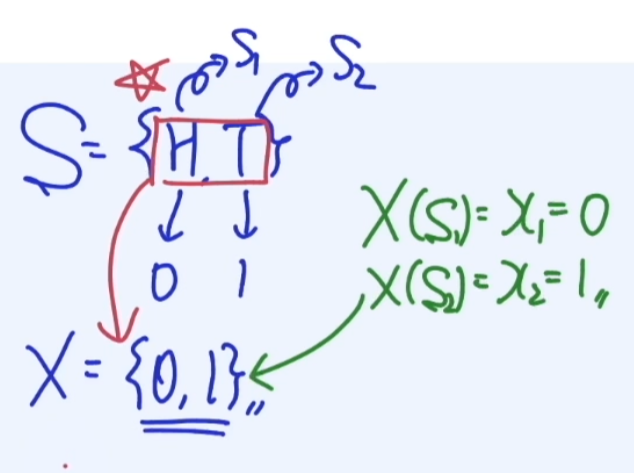
아래와 같이 앞면과 뒷면을 0 ,1로 정의하고 이를 S1, S2로 부르자.
또한 X라는 함수에 S1를 넣으면 이를 X1이라고 하고 값을 0으로 하자.
또한 X라는 함수에 S2를 넣으면 이를 X2이라고 하고 값을 1으로 하자.
이처럼 Sample Space를 실수에 대응시키는게 Ramdom variable 이다.
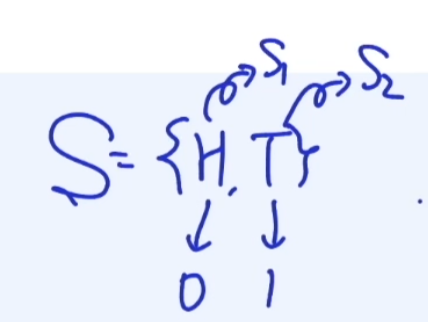

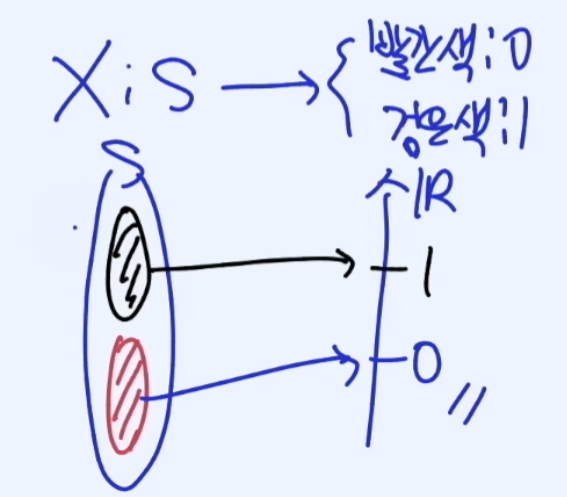
만약 카드 뽑기의 상황을 보자.

이떄 이 Sample space에 Outcome이 실수가 아니다.
이를 실수에 대응시켜 보자.
빨간색카드는 0, 검은색 카드는 1 이라고 할떄 X라는 확률변수는 이런식으로 만들수 있다.
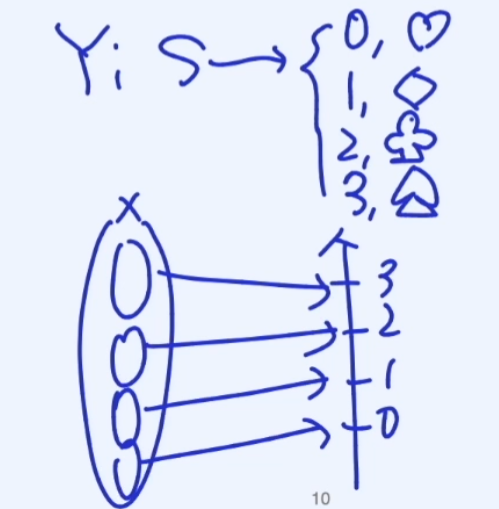
또한 하트, 다이아, 클로버, 스페이드의 경우 0,1,2,3으로 Y라는 확률 변수를 만들어보자.
또한 카드의 A부터 K까지를 숫자로 표현한 Z라는 확률 변수를 만들어보자.
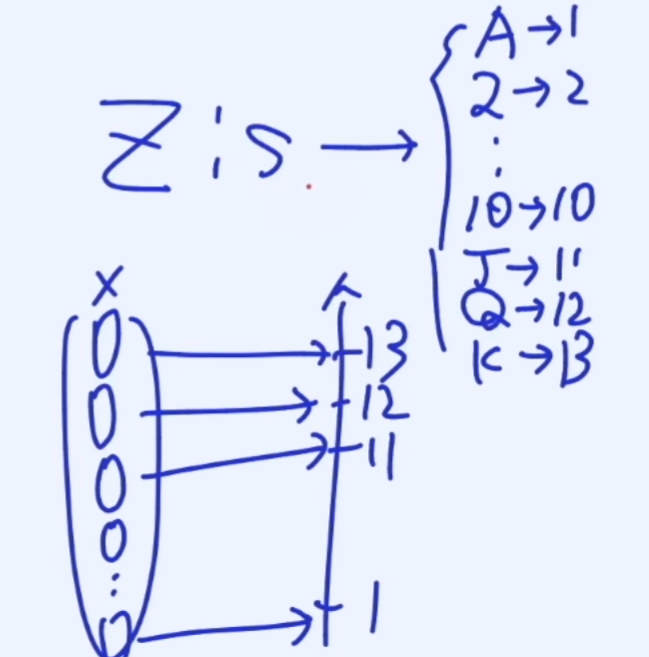
이처럼 구하고자 하는 바에 따라 여러개의 Ramdom variable을 만들 수 있다.
Continuous / Discrete R.V.
Sample space의 Outcome들이 정수와 같은 이산 숫자에 대응 되는 경우 이를 Discrete R.V. 를 말한다.
앞의 예시의 X,Y,Z의 확률변수도 이산 확률변수라고 볼 수 있다.
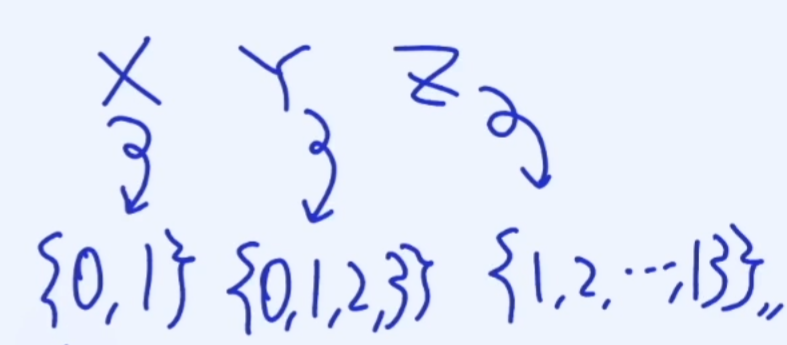
그러면 Continuous R.V의 예시를 보자
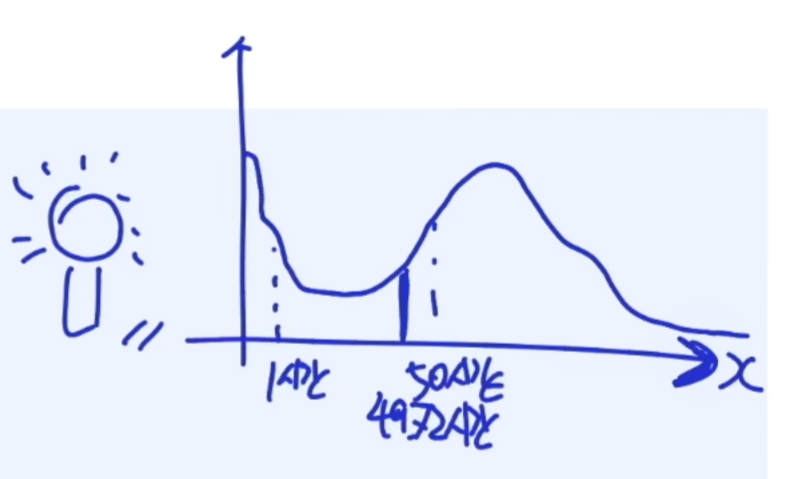
어떤 회사에서 전구의 수명을 측정하려고 한다
수명을 그래프로 표시하면 아래와 같다.
그래프를 보면 전구의 수명을 연속적인 시간에 연결한 것을 볼 수 있다.
'Statistics and Math' 카테고리의 다른 글
| CH04_07 이산, 연속 확률분포 (0) | 2022.09.28 |
|---|---|
| CH04_06 확률변수의 기댓값과 산포도 (0) | 2022.09.28 |
| 선형대수학(강의) (0) | 2022.09.28 |
| Ch04_04 베이즈 정리 (0) | 2022.09.27 |
| CH04_03 조건부 확률 (0) | 2022.09.27 |



