CH01_08 초월함수

1-3 Functions 초월함수

---

Transcendental Functions

 

Exponential Functions(지수 함수)

 

$$y = a^x$$

변수가 지수인 함수!

 

 

Logarithmic Functions(로그 함수)

 

$$y = log_a(x)$$

 

$$y = 2^x \ <==> \ y = log_2(x)(상호 \ 역함수) $$

 

CF) 역함수는 그래프 상에서 y = x 대칭이다! 

 

 

Trigonometric Functions(삼각 함수)

 

$$y = sin(x)  \\ y = cos(x) \\  y = tan(x)$$

 

 

삼각함수는 동경의 크기에 따라 변화하는 함수입니다.
동경위의 점과 원점, x축에 내린 발이 직각삼각형을 이루기 때문에 삼각함수라고 부릅니다.

 

위 그림에서 각의 크기가 θ인 동경 OX는 점 X(x,y)를 지납니다.
선분 OX의 길이를 r이라고 약속하면,
다음과 같은 삼각함수를 가집니다.

 

 

cf)

 

Cf) 추가적인 개념

 

​코시컨트(csc), 시컨트(sec), 코탄젠트(cot)

​

$$\csc(a)=\frac{1}{\sin(a)},\ \sec(a)=\frac{1}{\cos(a)},\ \cot(a)=\frac{1}{\tan(a)}$$

 

 

 

Hyperbolic Functions(쌍곡선 함수)

 

 

쌍곡선 함수는 각각 exp함수 (=밑이 e인 지수함수) 의 합, 차를 2로 나눈 값으로 정의된다.

쌍곡선 함수는 다음이 성립

 

 

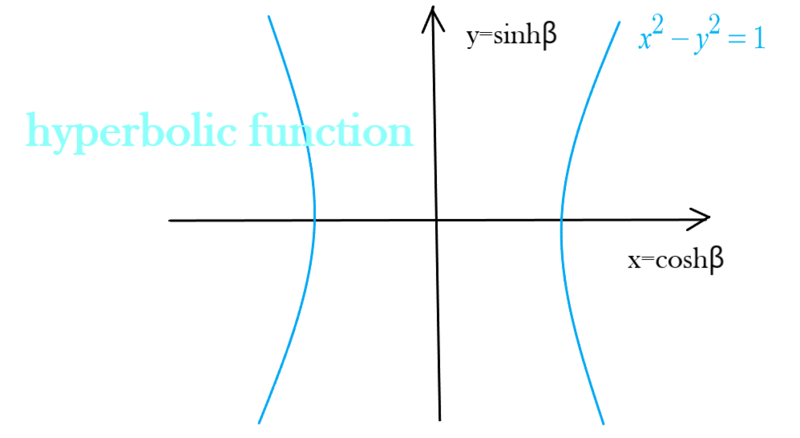
x= cosh β, y=sinh β 로 취급하여 그래프를 그린다면?
쌍곡함수의 그래프가 그려진다.