1-3 Functions, 선형함수
Linear Functions
Linear Functions은 2가지 뜻가짐
1. Linear Discision Boundary
2. Linearity
1. Linear Discision Boundary
성적 분포를 아래와 같이 찍을때, 선위쪽은 합격생, 아래쪽은 불합격생으로 나누는 방법.
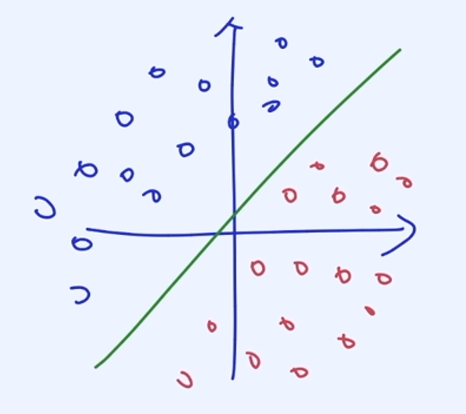
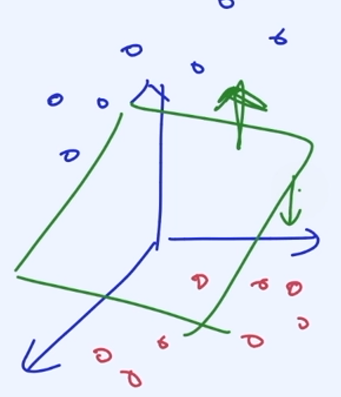
왼쪽은 좌표 평면에서 직선을 이용하여 나눔, 오른쪽은 평면을 이용해서 나눔
이러한 방법은 Linear한 결정 바운더리를 지니고 있다.
이와같은 함수들을 Linear Discision Boundary를 가진 함수라고 한다.
따라서 아래와 같이, 2. Linearity를 같추지 않더라도 Linear Discision Boundary를 가지고 있기때문에
Linear Function이다라고 부른다. 주로 딥러닝 에서 사용
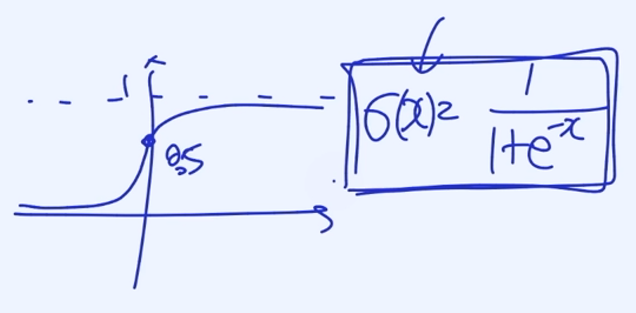
2. Linearity
하지만 일반적으로 Linear Function이라고 부르는 함수는 Linearity를 만족하는 함수이다.
Homogeneity
$$f(αx) = αf(x)$$
만약 x에 상수 a를 곱한 값에 함수를 적용한 것이,
함수에 적용한 뒤 상수 a를 곱해준 결과와 같으면,
동질성의 조건을 만족하는 것이다.
Additivity
$$f(x_1 + x_2) = f(x_1) + f(x_2)$$
만약 x1과 x2를 함수에 적용하기 전에 더한 것과,
함수에 각각 적용한 뒤 더한 것의 결과가 같으면,
중첩의 조건을 만족하는 것이다.
위를 하나의 수식으로 표현하면 다음과 같이 표현할 수 있다.
$$f(a_1x_1+a_2x_2)=a_1f(x_1)+a_2f(x_2)$$
예시
$$f(x) = ax$$
$$f(αx_1 + βx_2) = αf(x_1) + βf(x_2)$$
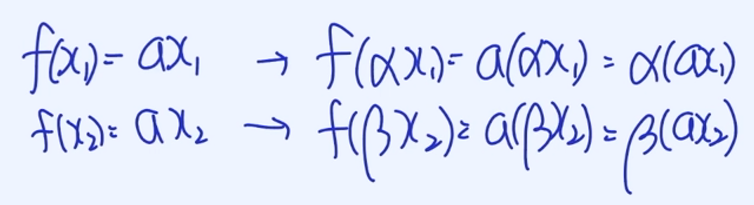
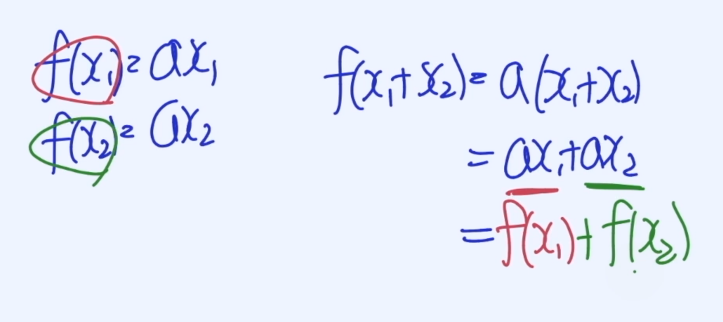
따라서 f(x)는 Linearity를 가진 Function이다.
$$g(x) = ax + b$$
$$g(αx_1 + βx_2) ≠ αg(x_1) + βg(x_2)$$
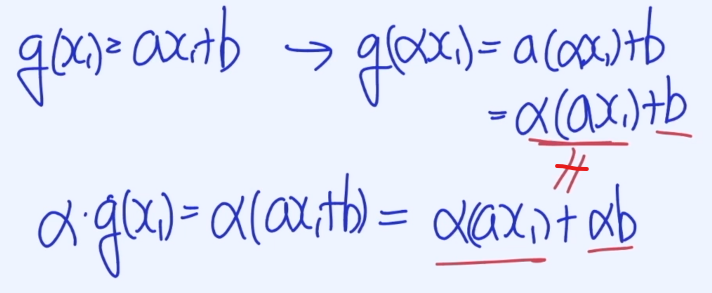
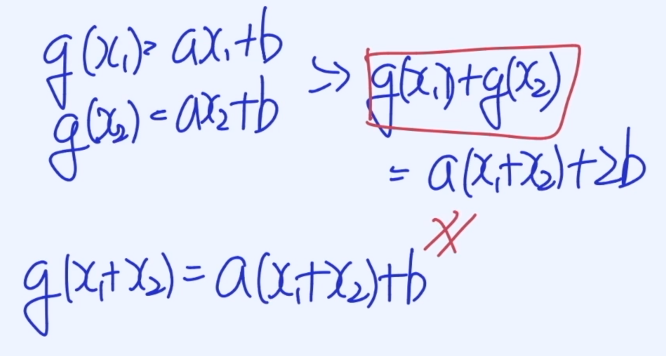
따라서 g(x)는 Linearity를 가지지 않은 함수 이다.
$$f(x) = x^2$$
이 함수는 1. Linear Disicion Bounadary 로 되지 않는다.
또한 2. Linearity 도 적용되지 않는 것을 볼 수 있다.
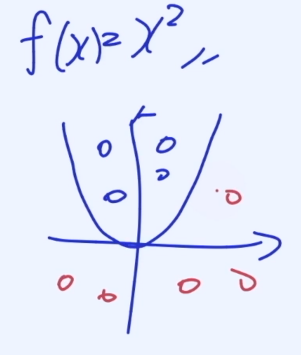

대부분의 함수는 Non-Linear한다. 하지만 Linear한 함수는 문제를 분석하고 설계해서 개선하는 시스템을 만들기 하기 쉽다. 따라서 상황을 분석할때 Non-Linear한 상황을 Linear하게 Approximate(근사화)해서 분석한다.
'Statistics and Math' 카테고리의 다른 글
| CH03_02 벡터의 연산2 (0) | 2022.09.27 |
|---|---|
| CH03(선형대수)_01 벡터의 연산1 (0) | 2022.09.27 |
| CH01_09 함수의 변형 (0) | 2022.09.27 |
| CH01_08 초월함수 (0) | 2022.09.27 |
| CH01_07. 대수함수 (0) | 2022.09.26 |



