1-3. Functions, 함수
Functions
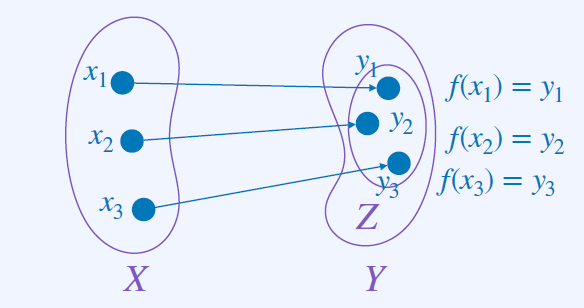
하나의 X는 Y에 대응, X는 두개의 Y에 대응되면 안된다.
X집합을 domain, Y집합을 co-domain.
소개팅 처럼 1대 1 대응을 해야한다.
두 집합 X, Y에 대해 ∀x ∈ X가 y ∈ Y에 오로지 하나만 대응되는 관계

Injective Function
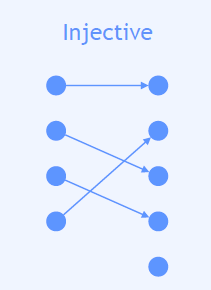
같은 y는 한 번씩만 대응
many-to-one NOT OK
y1 = y2 ⟶ x1 = x2
Surjective Function
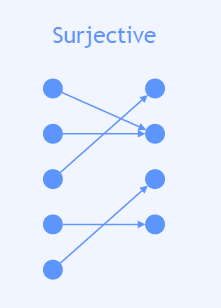
Codomain = Range
모든 y는 적어도 하나의 x에 대응
Bijective Function
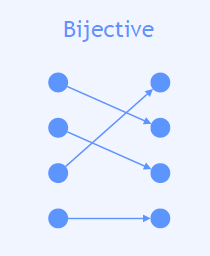
Injective ∧ Surjective
one-to-one correspondence
Composite Functions

$$h = (g ∘ f )(x) = g( f(x))$$
Inverse Functions
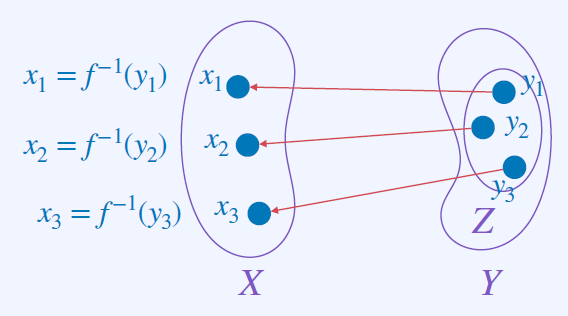
$$f(x1) = y1⟶f ^−1(y1) = x1\\f(x2) = y2⟶f ^−1(y2) = x2\\f(x3) = y3⟶f ^−1(y3) = x3$$
bijective Function을 만족해야 Inverse Functions을 사용할 수 있다.
'Statistics and Math' 카테고리의 다른 글
| CH01_08 초월함수 (0) | 2022.09.27 |
|---|---|
| CH01_07. 대수함수 (0) | 2022.09.26 |
| CH01_05. 파티션 (0) | 2022.09.26 |
| CH01_04 집합의 연산 (1) | 2022.09.26 |
| CH01_03. 집합의 포함관계 (1) | 2022.09.26 |



