1-3 Functions, Translations(대칭이동) and Transformations
Translations of Functions
Horizontal Translations
$$y = f(x)⟶y = f(x − α)$$
Vertical Translations
$$y = f(x)⟶y − β = f(x)$$
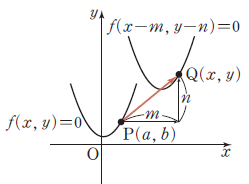
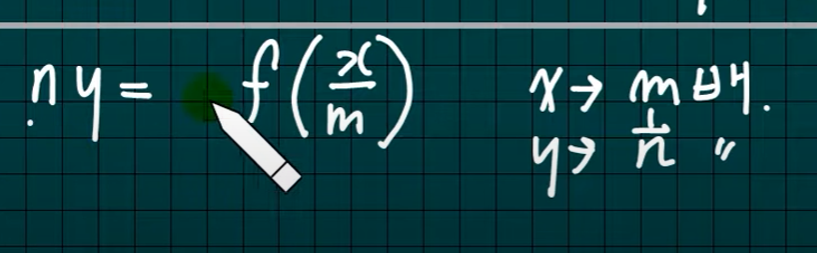
방정식이 f(x, y)=0 인 도형을 x축 방향으로 m만큼, y축 방향을 n만큼 평행이동한 새로운 도형의 방정식은 다음과 같다.
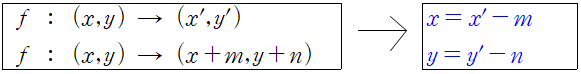
⇒ f(x, y)=0 → f(x-m, y-n)=0
y=f(x) → y-n=f(x-m)
x 대신에 x-m , y 대신에 y-n 대입
f(x, y)=0 → f(x+a, y+b)=0
⇒ 도형 f(x, y)=0을 x축의 방향으로 –a만큼, y축의 방향으로 –b만큼 평행이동
(주의, 도형의 이동은 점의 이동과 달리 반대부호를 붙여서 대입해야 함)
Transformations of Functions
(함수의 확장, 축소를 이야기 함, 영어로 'Dilation'이라고도 한다)

Horizontal Transformations
$$y= f(x)⟶y = f(α ⋅ x)$$
Vertical Transformations
$$y = f(x)⟶β ⋅ y = f(x)$$
Horizontal Dilation
The horizontal dilation (also known as horizontal scaling) of a function either stretches/shrinks the curve horizontally. It changes a function y = f(x) into the form y = f(kx), with a scale factor '1/k', parallel to the x-axis. Here,
- If k > 1, then the graph shrinks.
- If 0 < k < 1, then the graph stretches (x축 방향으로).

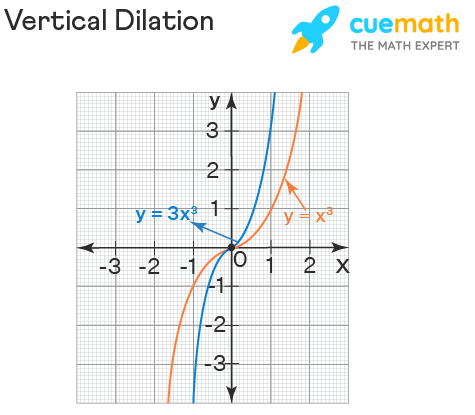
Vertical Dilation
The vertical dilation (also known as vertical scaling) of a function either stretches/shrinks the curve vertically. It changes a function y = f(x) into the form y = k f(x), with a scale factor 'k', parallel to the y-axis. Here,
- If k > 1, then the graph stretches. (y축 방향으로)
- If 0 < k < 1, then the graph shrinks.
참고 영상) 함수 그래프 자유자재로// 함수의 확대와 축소 | 함수의 여러가지 변환
https://www.youtube.com/watch?v=RaLS2I6gadg
x축 방향으로 1/m배 확대,
y축 방향으로 n배 확대
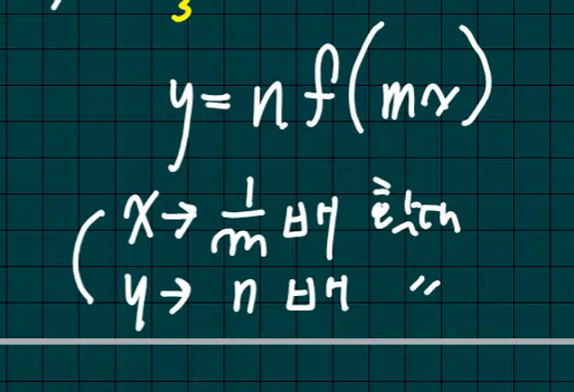
Reflections of Functions
Horizontal Transformations ( y축 대칭)
$$y = f(x)⟶y = f(α ⋅ x)$$
Vertical Transformations (x축 대칭)
$$y = f(x)⟶β ⋅ y = f(x)$$
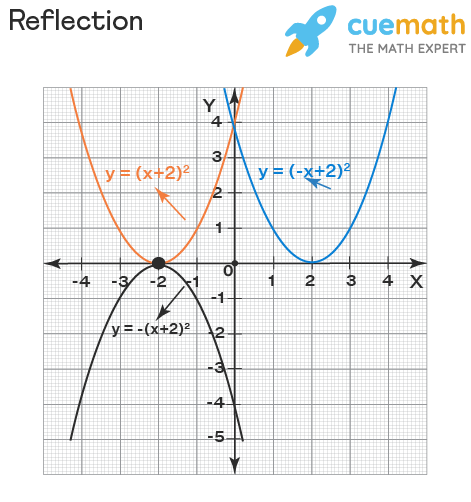
A reflection of a function is just the image of the curve with respect to either x-axis or y-axis. This occurs whenever we see the multiplication of a minus sign happening somewhere in the function. Here,
- y = f(-x) is the reflection of y = f(x) with resepct to the y-axis.
- y = - f(x) is the reflection of y = f(x) with respect to the x-axis.
Observe the graph below where the original graph y = (x + 2)2 is reflected with respect to each of the x and y axes
Rotation across the Origin (원점을 기준으로 대칭)
$$y = f(x)⟶y = − f(−x)$$
Even / Odd Functions
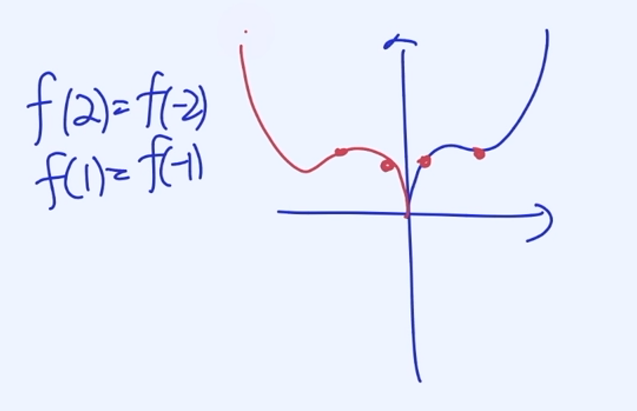
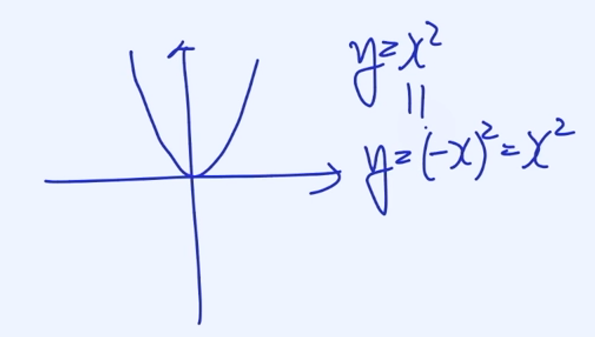
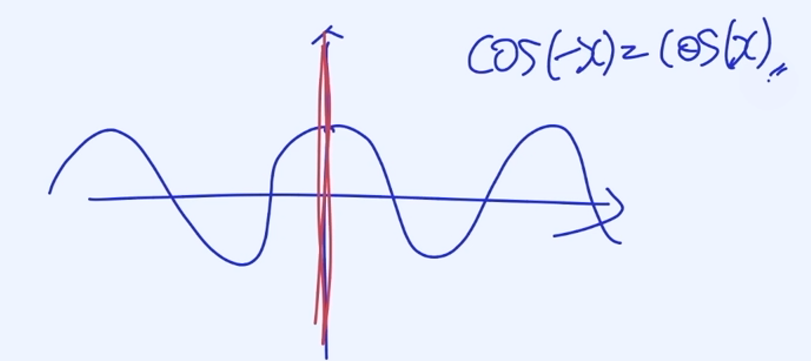
Even Functions (우 함수)
$$f(−x) = f(x)$$
y축 대칭
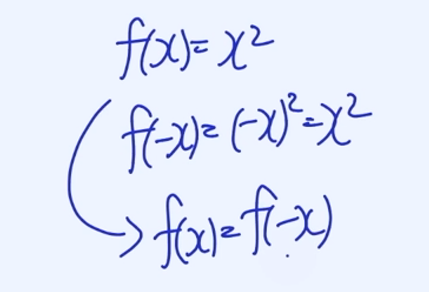
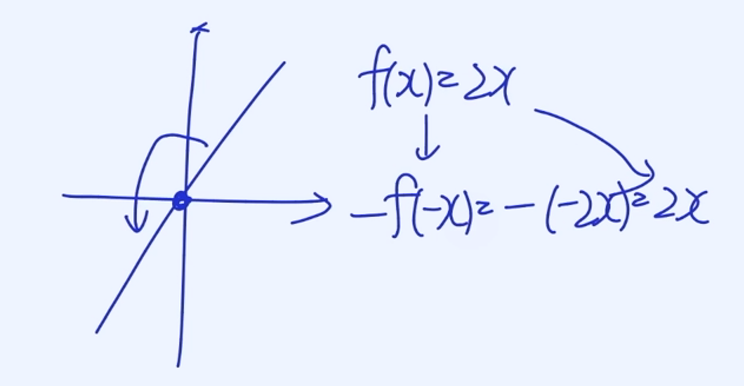
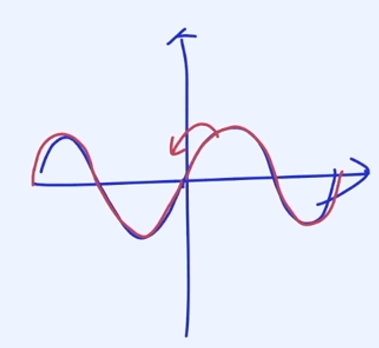
Odd Functions(기함수)
f(−x) = − f(x)
원점 대칭

'Statistics and Math' 카테고리의 다른 글
| CH03(선형대수)_01 벡터의 연산1 (0) | 2022.09.27 |
|---|---|
| CH01_10. 선형함수 (0) | 2022.09.27 |
| CH01_08 초월함수 (0) | 2022.09.27 |
| CH01_07. 대수함수 (0) | 2022.09.26 |
| CH01_06. 함수 (0) | 2022.09.26 |



