머신러닝에서 쓰이는 수학
1. 선형대수
- 행렬
2. 미적분학 (미분 위주)
- 최적화 (오차를 최소화)
3. 통계
- 데이터 이해
- 패턴
4. 확률
- 예측 / 가능성
선형 대수학을 배우는 이유
파이썬 numpy array 같은 경우라던지, 행렬 등의 개념이 사용되는 것이 많다.
선형대수학 : 일차식이나 일차 함수를 공부하는 학문
복잡한 선형 시스템을 행렬과 벡터로 쉽게 표현 가능

일차식과 일차함수
(n차) 다항식
● 일차식 : 가장 높은 차수가 1인 다항식
● n차식 : 가장 높은 차수가 n인 다항식
e.g. 3차 다항식



(n차)함수
● 일차 함수
y는 x에 대한 함수

함수 f는 x에 대한 함수

● 3차 함수

일차식 표기법
변수 개수에 따른 함수 표현
● 변수 x, y에 대한 함수(예시)
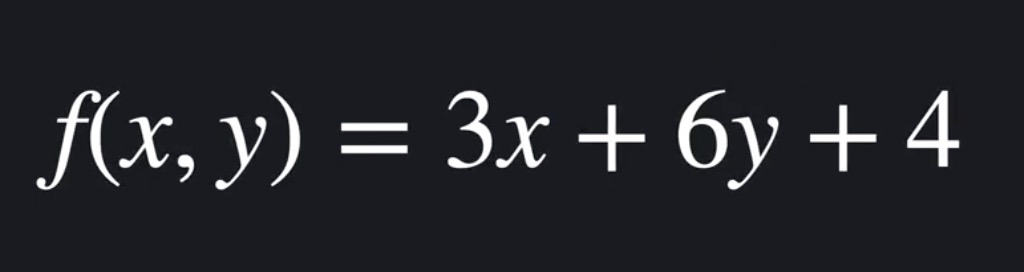
● 변수 여러 개에 대한 함수 표현

행렬
행렬(Matrix)
● 행렬A의 원소 12개
- 3행(row), 4열(column)
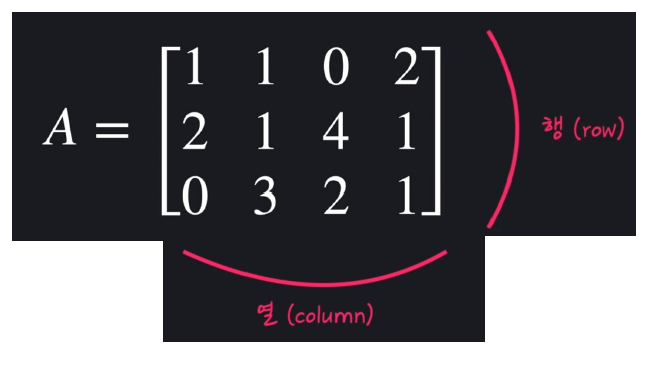
=> 3 X 4 행렬
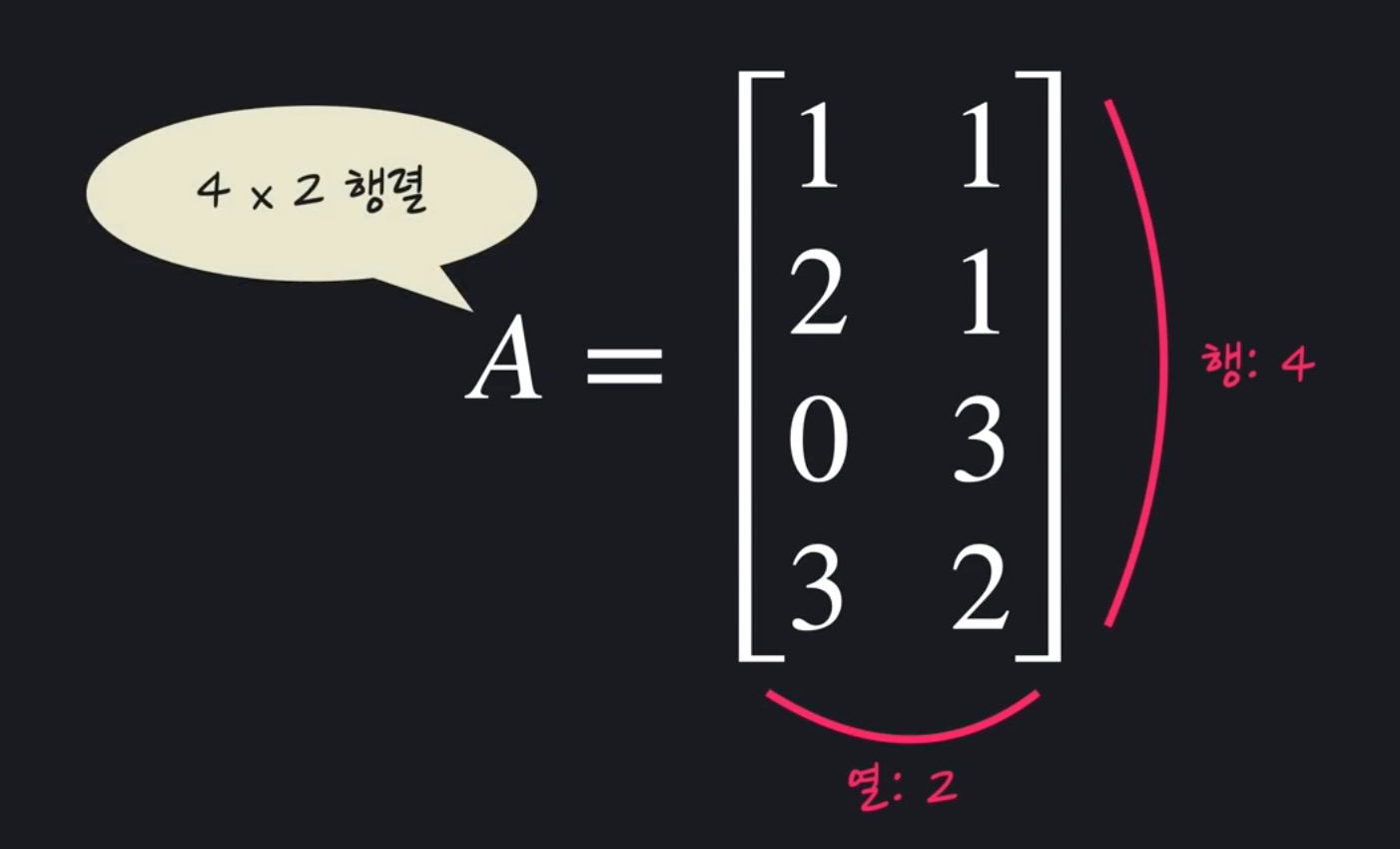
=> 4 X 2 행렬
행렬의 원소 표현
● 행렬A의 i행, j열에 위치한 원소를 표현하려면 : Aij

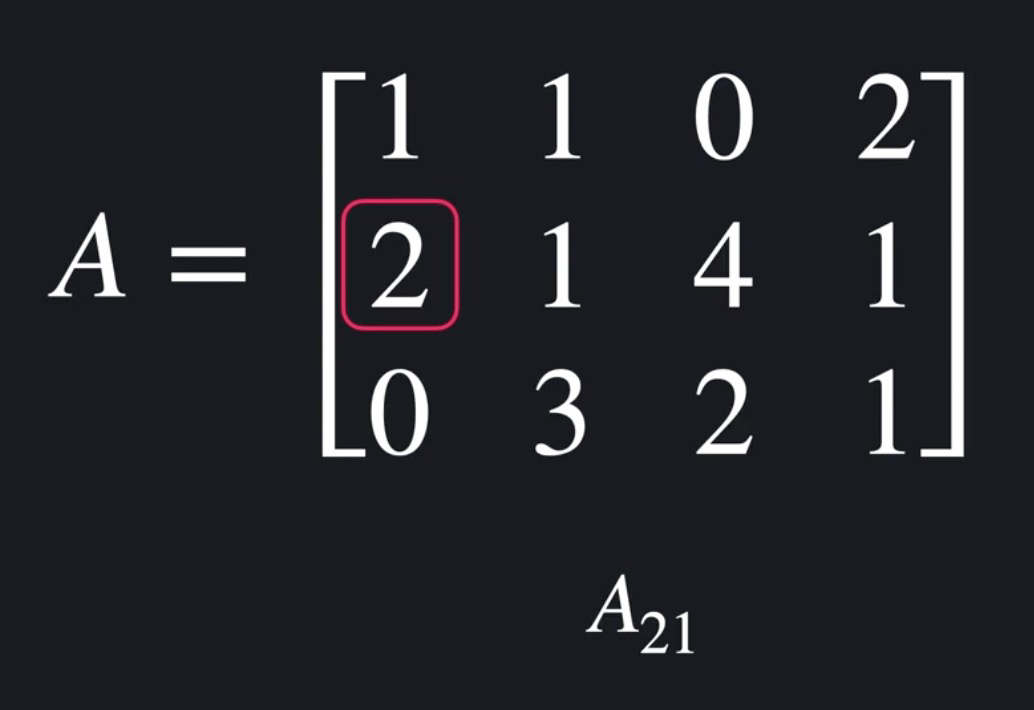

실습 - 넘파이로 행렬 사용하기

import numpy as np
A = [[0,1,-1],[1,2,3],[2,1,0],[-1,2,-4]]
B = [[0,2],[1,1],[-1,-2]]
np.array(A)
array([[ 0, 1, -1],
[ 1, 2, 3],
[ 2, 1, 0],
[-1, 2, -4]])
np.array(B)
array([[ 0, 2],
[ 1, 1],
[-1, -2]])
A[1][1] => 2
A[3][0] => -1
행렬의 원소 표현
● m x n 행렬의 원소 표현
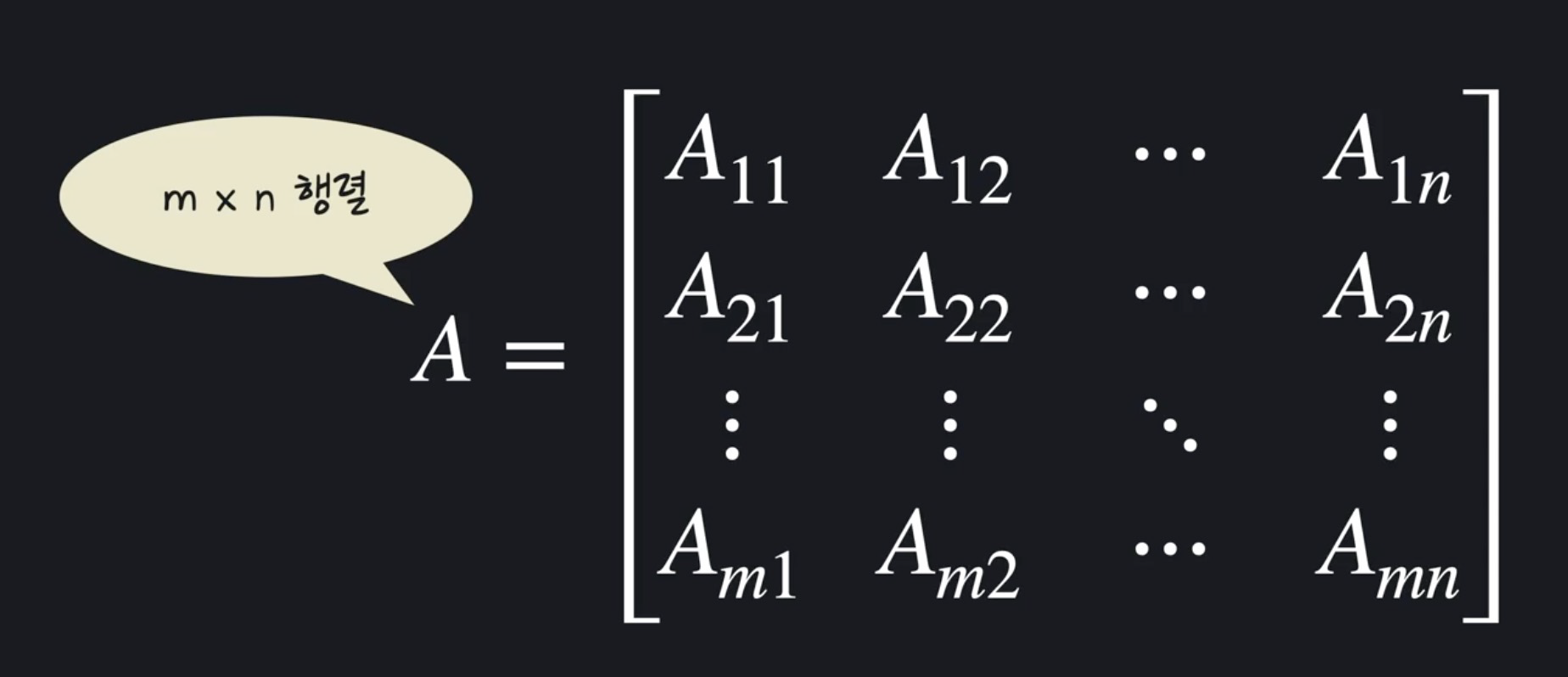
벡터
벡터(Vector)
● 벡터 : 행이 하나거나 열이 하나인 행렬
- 보통 벡터라 하면 열벡터를 의미함
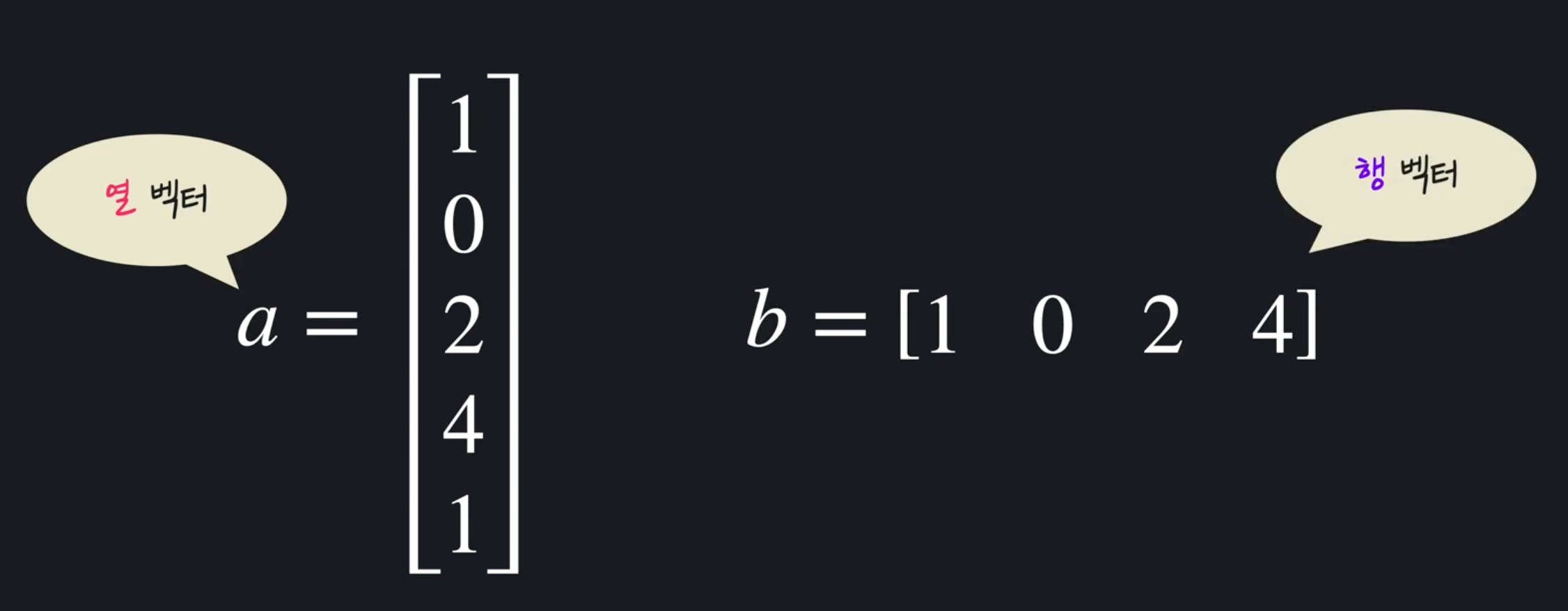
● 차원
- a는 5차원 열 벡터, b는 4차원 행 벡터
● m차원 벡터

● 보통 행렬은 대문자, 벡터는 소문자로 표현

행렬 덧셈과 곱셈
행렬의 덧셈
● 같은 위치에 있는 원소들을 더해준다.

행렬의 스칼라 곱
● 스칼라곱
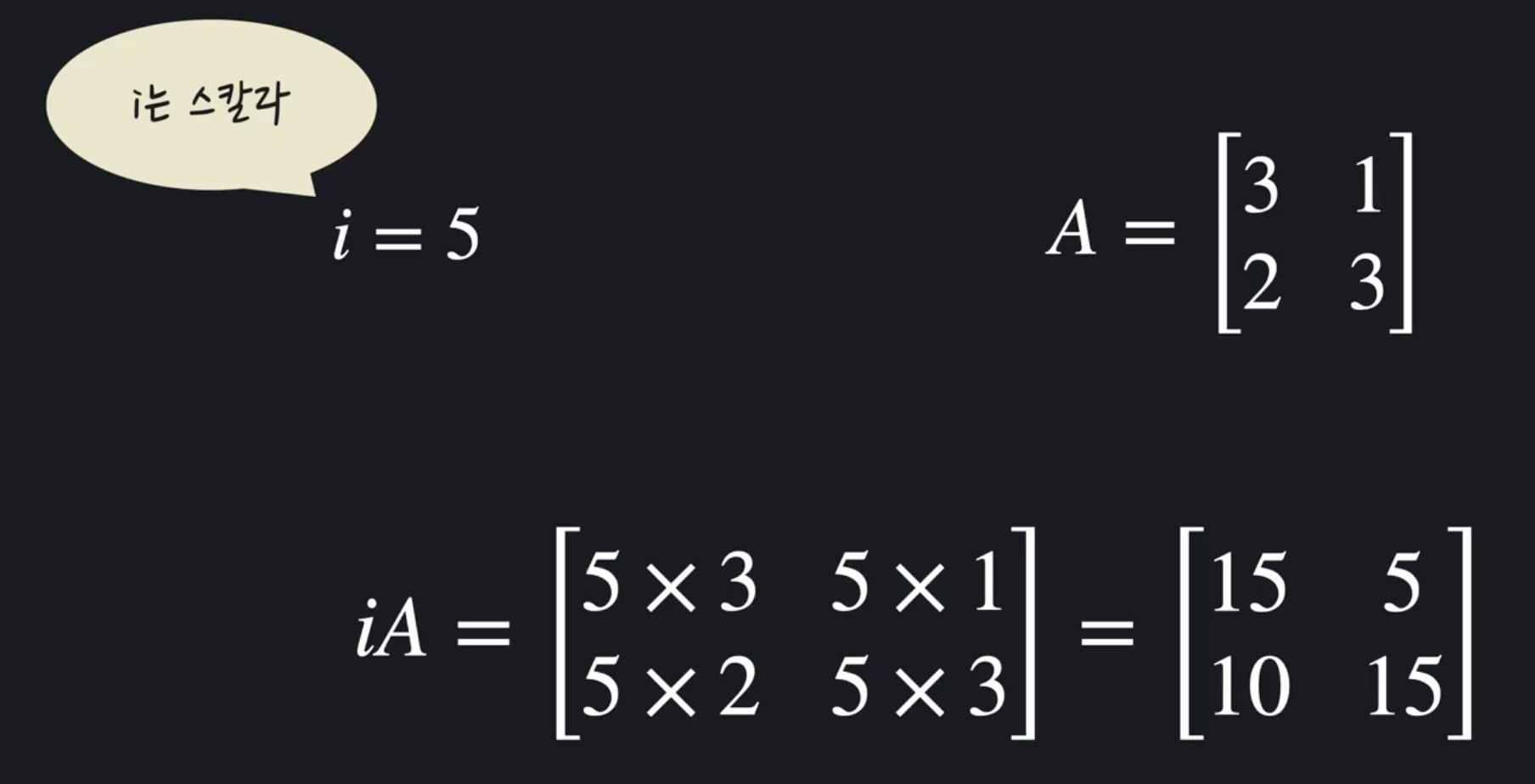
두 행렬의 곱 – 내적곱, 외적곱
우리는 내적곱만 배울 예정
두 행렬의 내적 곱
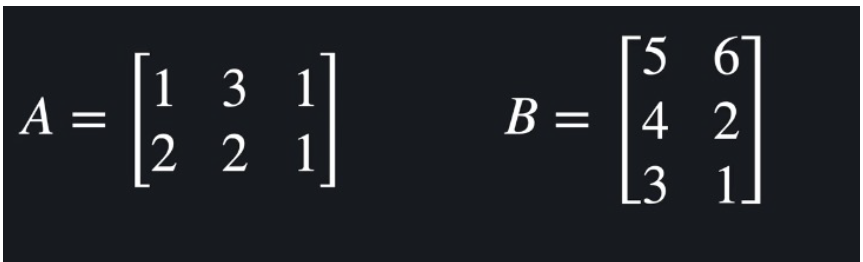
A(2 X 3) X B(3 X 2) => shape (2 X 2)
1 * 5 + 3 * 4 + 1 * 3 = 20 1 * 6 + 3 * 2 + 1 * 1 = 13
2 * 5 + 2 * 4 + 1 * 3 = 21 2 * 6 + 2 * 2 + 1 * 1 = 17
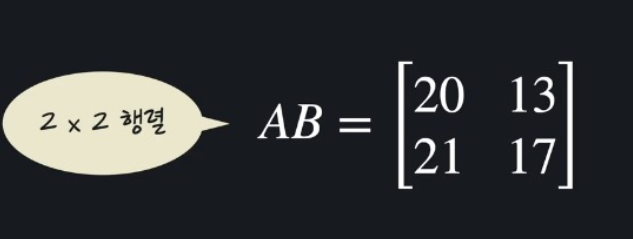
두 행렬의 내적곱
파이썬에서는 @ 으로 표시한다. 넘파이에서는 dot으로 표시한다.


두 행렬의 내적곱 - 예시

실습 - 넘파이로 행렬 사용하기

행렬곱(@) / 스칼라 곱(*)
A = np . array(
[[ 1 , - 1 , 2 ],
[ 3 , 2 , 2 ]
] )
B = np . array( [
[ 0 , 1 ] ,
[ - 1 , 1 ] ,
[ 5 , 2 ]
] )
C = np . array( [
[ 2 , - 1 ],
[ - 3 , 3 ]
] )
D = np . array( [
[ - 5 , 1 ] ,
[ 2 , 0 ]
] )
(2*A) @ (-1*B) @ (3*C + D)array([[ 34, -28],
[ 110, -130]])
행렬 연산 퀴즈

질문1
a13 = -1 + -2 = -3
질문2
a11 = 1 * 3 + 2 * 1 + -1 * 2 = 3
질문3
a12 = 1 * 2 + 2 * 1 + -1 * -1 = 5
질문4
AB shape ( 3 x 3 ) @ ( 3 x 2) = ( 3 x 2 )
두 행렬 요소 별 곱하기 : o

두 행렬 요소 별 곱하기 : o – 파이썬 넘파이로 구현

실습 – 넘파이로 행렬 연산하기
np.dot(A , B) 와 A @ B가 동일한 내적의 곱인 것을 유의하며 보자.
A = np.array(
[[1, -1, 2],
[3, 2, 2],
[4, 1, 2]])
B = np.random.rand(3,3)
A
array([[ 1, -1, 2],
[ 3, 2, 2],
[ 4, 1, 2]])
B
array([[0.52029652, 0.74584724, 0.32701989],
[0.05597946, 0.51938929, 0.59335944],
[0.67059721, 0.67772168, 0.378086 ]])
A + B
array([[ 1.52029652, -0.25415276, 2.32701989],
[ 3.05597946, 2.51938929, 2.59335944],
[ 4.67059721, 1.67772168, 2.378086 ]])
5 * A
array([[ 5, -5, 10],
[15, 10, 10],
[20, 5, 10]])
np.dot(A,B)
array([[1.80551148, 1.58190132, 0.48983245],
[3.01404292, 4.63176365, 2.92395055],
[3.47835998, 4.8582216 , 2.657611 ]])
A @ B
array([[1.80551148, 1.58190132, 0.48983245],
[3.01404292, 4.63176365, 2.92395055],
[3.47835998, 4.8582216 , 2.657611 ]])
특수행렬: 전치행렬, 단위행렬, 역행렬
전치 행렬(Transposed Matrix)
● 행과 열을 서로 바꾸어주는 것
● 행렬 연산 시 행 수와 열 수를 맞춰주기 위해 사용 (2 x 3) (5 x 3).T => (3 x 5)
파이썬에서 A.T, A.transposed()로 사용
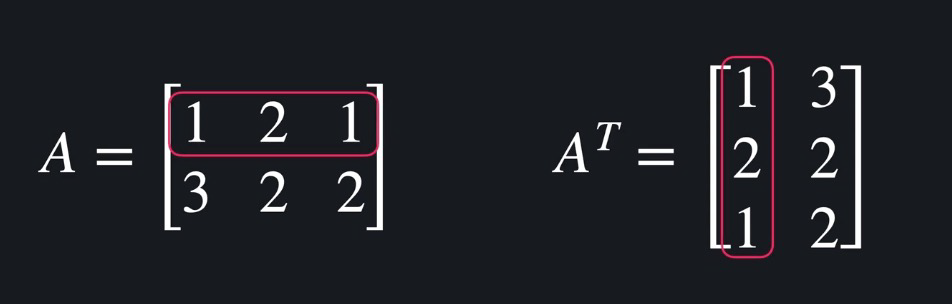
단위 행렬(identity matrix)
● 대각 행렬 값이 모두 1인 행렬
● 어떤 행렬A에 단위 행렬을 곱하면 그대로A가 된다.


역행렬(Inverse Matrix)
● 행렬 자기 자신과 곱했을 때 단위 행렬이 나오는 행렬
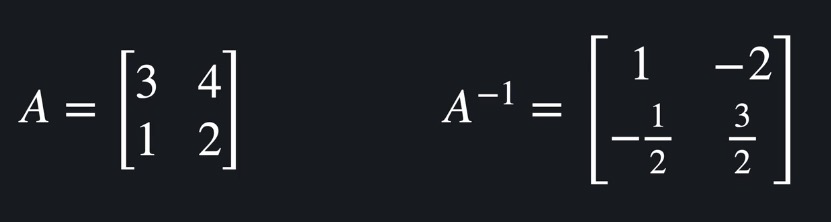
A x A-1 = I
실습1 – 넘파이로 전치, 단위, 역행렬 사용하기
A = np.array(
[[1, -1, 2],
[3, 2, 2],
[4, 1, 2]])
A_tranpose = A.T
A.T
array([[ 1, 3, 4],
[-1, 2, 1],
[ 2, 2, 2]])
A.transpose()
array([[ 1, 3, 4],
[-1, 2, 1],
[ 2, 2, 2]])
선형 대수학이 머신러닝에 사용되는경우
● 복잡한 수식을 행렬과 벡터로 요약해서 표현할 수 있다.
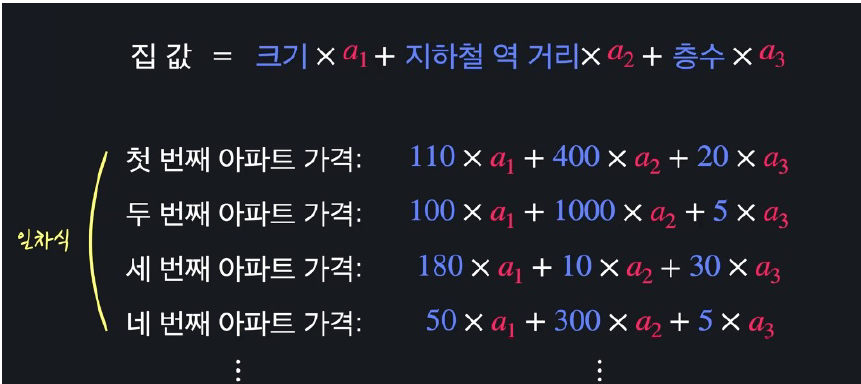

선형대수학과 머신러닝 요약
● 선형대수학은 일차식, 일차 함수, 행렬, 벡터를 다루는 학문이다.
● 머신러닝을 할 때 데이터를 일차식으로 표현하는 경우가 많다.
● 행렬과 벡터를 이용하면 정돈된 형태로 효율적 계산이 가능하다.
'Statistics and Math' 카테고리의 다른 글
| CH04_06 확률변수의 기댓값과 산포도 (0) | 2022.09.28 |
|---|---|
| CH04_05 확률변수 (0) | 2022.09.28 |
| Ch04_04 베이즈 정리 (0) | 2022.09.27 |
| CH04_03 조건부 확률 (0) | 2022.09.27 |
| CH04_02. 확률의 계산 (0) | 2022.09.27 |



