Numpy (Numeric python)
- 패키지 이름과 같이 수리적 파이썬 활용을 위한 파이썬 패키지
- 선형대수학 구현과 과학적 컴퓨팅 연산을 위한 함수를 제공
- (key) nparray 다차원 배열을 사용하여 벡터의 산술 연산이 가능
- 브로드캐스팅을 활용하여 shape(형태 혹은 모양)이 다른 데이터의 연산이 가능
- 기존 언어에서는 제공 X
- 굉장히 파워풀한 기능으로서 빅데이터 연산에 굉장히 효율이 좋음
1. Numpy 설치와 import
- 선행 학습을 통해 클래스와 함수에서 클래스를 불러들여 사용할 수 있다고 배웠다.
- 다만 직접 작성한 클래스가 아닐경우, 그리고 현재 컴퓨터에 사용해야 할 패키지가 없을경우,
- 간단한 명령어로 설치가능하다.
- pip, conda 명령어 : python 라이브러리 관리 프로그램으로 오픈소스라이브러리를 간편하게 설치 할 수 있도록 하는 명령어
콘솔창에서 실행 시
pip install [패키지명] 혹은 conda install [패키지명]
주피터 노트북으로 실행 시
!pip install [패키지명]
아나콘다 환경으로 python 환경설정 시 기본적으로 Numpy 설치가 되어있음
# 주피터 노트북에서 Numpy 설치 # pip 설치 명령어 # !
=> anaconda prompt 에 바로 안적어도, !를 앞에 붙여서 설치할 수 있다.
!pip install numpy
Requirement already satisfied: numpy in c:\users\jin seong eun\anaconda3\lib\site-packages (1.21.5)
>> 이미 설치되어 있어서 이렇게 나온다!
# Numpy 사용을 위해 패키지 불러들이기
# 관례적으로 np라는 약자를 많이 사용한다.
# 파이썬을 사용하는 대부분의 유저들이 사용하고 있는 닉네임이니 이건 꼭 지켜서 사용해주시는 것을 추천
# 외워 두면 편하다.
import numpy as np
2. 데이터분석을 위한 잠깐의 선형대수학
- numpy는 기본적으로 수리적 컴퓨팅을 위한 패키지 입니다. 선형대수학을 약간만 이해한다면 데이터를 훨씬 더 깊이있게 다룰 수 있습니다.

# scalar : 숫자 하나 0, 10 , -1, 2, 3,
# vector : 크기와 방향이 있는 스칼라 값의 눈금
[1, 2, 3, 4, 5] --> 리스트도, 크기 5개, 방향 오른쪽 ----> 고로 리스트도 벡터 데이터이다.
a = "안녕하세요" ---> 문자열도 어절단위 5개, 방향은 오른쪽 ----> 고로 문자열은 벡터 데이터이다.
# Matrix : 행열이라고 부름, 행과 열이 있는 데이터, 테이블 형태의 데이터,
ex) 엑셀: 전형적인 메트리스 데이터
# Tensor : 메트리스 형태의 데이터가 축이 하나 추가되었다. matrix + 축하나
ex) 컬러이미지, 동영상
3. 데이터의 구분에 따른 표현 방법과 예시
3.0.1 스칼라
1, 3.14, 실수 혹은 정수
3.0.2 벡터
[1, 2, 3, 4], 문자열
3.0.4 3 X 4 매트릭스
[[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 0, 11, 12]]
3.0.4 2 X 3 X 4 텐서 --> 2 X (3 X 4)
[[[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 0, 11, 12]],
[[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 0, 11, 12]]]
3.1 데이터로 표현한 선형대수학

3.2 데이터 형태에 따른 사칙연산
스칼라 +, -, *, / -> 결과도 스칼라 1+1 =2
벡터 +, -, 내적
-> +, - 결과는 벡터, X 연산 내적 결과는 스칼라
매트릭스 +, -, *, /
텐서 +, -, *, /
3.3 데이터분석에 자주 사용하는 특수한 연산
벡터와 벡터의 내적

# 벡터의 곱으로 했는데 값이 스칼라이다.
3.3.1 벡터와 벡터의 내적이 이루어지려면
1. 벡터가 마주하는 shape의 갯수(길이)가 같아야 합니다.
(1,4) * (4,1) = 4)*(4 가 같아야 하고 결과값은 (1, 1)
만약 매트리스 라면?
(4, 5) * (5 ,6) => (4, 6)으로 나온다 내적 5) * (5 이므로 가능하다!
2. 연산 앞에 위치한 벡터는 전치(transpose) 되어야 합니다.
전치는 축방향 대로 데이터를 뒤집는것을 말한다.
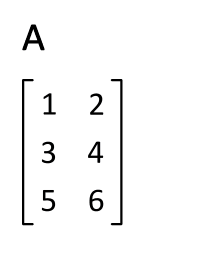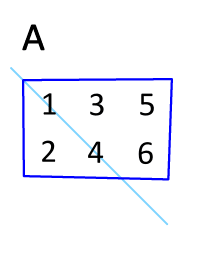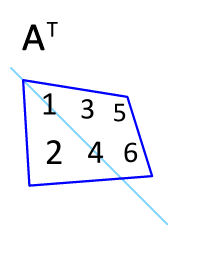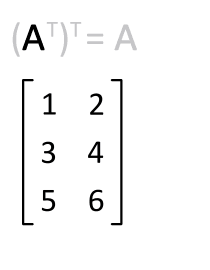
3.3.2 벡터 내적으로 방정식 구현

4. 브로드캐스팅
파이썬 넘파이 연산은 브로드캐스팅을 지원한다.
벡터연산 시 shape이 큰 벡터의 길이만큼 shape이 작은 벡터가 연장되어 연산된다.
벡터 + 스칼라 => 벡터 요소에 스칼라 값을 더한다.
(0,1,2) (5,5,5) ---> 1,1의 5 스칼라를 5,5,5의 벡터로 변경하였다.
벡터 + 벡터 ---> 0,1,2를 3 x 1 x 3형태로 변환!

5. Numpy function(유니버셜 함수)
numpy는 컴퓨팅연산을 위한 다양한 연산함수를 제공한다.연산함수 기본구조
ex) np.sum(연산대상, axis=연산방향)
dtype( )
5.1 수리연산
- prod()
- dot()
- sum()
- cumprod()
- cumsum()
- abs()
- sqaure()
- sqrt()
- exp()
- log()
5.2 통계연산
- mean()
- std()
- var()
- max()
- min()
- argmax()
- argmin()
5.3 로직연산
- arange()
- isnan()
- isinf()
- unique()
5.4 기하
- shape()
- reshape()
- ndim()
- transpose()
각종 연산 함수 참고: https://numpy.org/doc/stable/reference/routines.math.html 공식 링크에 더 있음
numpy 함수 실습
# 함수 예제를 위한 데이터셋
test_list = [1, 2, 3, 4]
test_list2 = [[1, 3], [5, 7]]
test_flist = [1, 3.14, -4.5]
test_list_2nd = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
test_list_3rd = [[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[1, 2, 3, 4],
[5, 6, 7, 8]]]
test_exp = [0, 1, 10]
test_nan = [0, np.nan, np.inf]
np.prod(test_list) # 1, 2, 3, 4, ==> 1 x 2 x 3 x 4
>>> 24
# 합연산
np.sum(test_list) # 1 + 2 + 3 + 4
>>> 10
# 누적곱연산
np.cumprod(test_list)
# 각 원소가 곱해지고 있는 과정을 보여줌, 그래서 백터로 표현
# 1 , 1 x 2 , 1 x 2 x 3, 1 x 2 x 3 x 4
array([ 1, 2, 6, 24], dtype=int32)
# 누적합연산
# 누적 일별 매출 구하라, 누적 수익률-> 이럴 떄 필요
# 각 원소가 더해지고 있는 과정을 표현
np.cumsum(test_list)
array([ 1, 3, 6, 10], dtype=int32)
# test_flist를 한번 보자
test_flist
>>> [1, 3.14, -4.5]
# 절대값
np.abs(test_flist)
>>> array([1. , 3.14, 4.5 ])
# 제곱
np.square(2)
>>> 4
# 루트
np.sqrt(2)
>>> 1.4142135623730951
# exp 자연로그e
np.exp(2)
>>> 7.38905609893065
# 로그
np.log(2)
>>> 0.6931471805599453
6. 통계값
test_list
>>> array([1, 2, 3, 4])
# 평균
np.mean(test_list)
>>> 2.5
# 표준편차
np.std(test_list)
>>> 1.118033988749895
# 분산
np.var(test_list)
>>> 1.25
# 최대값
np.max(test_list)
>>> 4
# 최소값
np.min(test_list)
>>> 1
test_list_2nd
>>> [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
# 최대값 존재하고 있는 인덱스 넘버를 리턴 argmax( )
# 자주 사용합니다.
# 출력값이 인덱스
# 제일 큰 값 있는 위치 찾아줌
# 연산을 통해 결과값을 내면 거기에 있는 최대값을 찾거나,
# 두가지 확률값을 비교를 통해서 더 큰 값 찾기
np.argmax(test_list_2nd)
>>> 8
# 인덱스 넘버 8번 위치를 반환해줌
# 최소값 인덱스 argmin( )
# argmax보다는 덜 쓰이지만 자주 보임
np.argmin(test_list_2nd)
>>> 0
# 범위설정 arange( )
# (시작포인트, 마지막포인트 + 1, 스텝수)
# range() 함수와 동일하게 작동함
# for i in range(0, 100, 10):
# print(i)
# range와 비슷하게 numpy에서 사용하는 함수
np.arange(0,21,5)
>>> array([ 0, 5, 10, 15, 20])
# 범위 데이터 생성
# (시작포인트, 마지막포인트 + 1, 데이터갯수)
# 0과 마지막 포인트 사이에 데이터 갯수를 만들어줌
# 그래프 그릴떄 x 축 값으로 많이 사용
# 그래프가 스무스하게 나오게 할 수 있다.
np.linspace(0,10,50)
>>> array([ 0. , 0.20408163, 0.40816327, 0.6122449 , 0.81632653,
1.02040816, 1.2244898 , 1.42857143, 1.63265306, 1.83673469,
2.04081633, 2.24489796, 2.44897959, 2.65306122, 2.85714286,
3.06122449, 3.26530612, 3.46938776, 3.67346939, 3.87755102,
4.08163265, 4.28571429, 4.48979592, 4.69387755, 4.89795918,
5.10204082, 5.30612245, 5.51020408, 5.71428571, 5.91836735,
6.12244898, 6.32653061, 6.53061224, 6.73469388, 6.93877551,
7.14285714, 7.34693878, 7.55102041, 7.75510204, 7.95918367,
8.16326531, 8.36734694, 8.57142857, 8.7755102 , 8.97959184,
9.18367347, 9.3877551 , 9.59183673, 9.79591837, 10. ])
# 아래는 검증할 떄 사용하는 함수들
test_nan
>>> [0, nan, inf]
# 결측 확인(데이터가 있어야 할 위치에 데이터가 없을 경우 NaN, 결측치)
# 검증할떄 쓰인다.
# Nan 값이 있는지 isnan( )
np.isnan(test_nan)
>>> array([False, True, False])
# 발산 확인, 무한대 인지 확인 isinf( )
np.isinf(test_nan)
>>> array([False, False, True])
test_list_3rd
>>> [[[1, 2, 3, 4], [5, 6, 7, 8]],
[[1, 2, 3, 4], [5, 6, 7, 8]],
[[1, 2, 3, 4], [5, 6, 7, 8]]]
# 고유값 확인 , 중복값 제거해준다. unique ( )
np.unique(test_list_3rd)
>>> array([1, 2, 3, 4, 5, 6, 7, 8])
# 데이터 구조(모양)확인 shape( )
np.shape(test_list_3rd)
>>> (3, 2, 4) # 텐서데이터 이다.
# 데이터 shape 변경 reshape( )
# 어떤 조건에서 reshape가능한가? 데이터 내부에 존재하는 속성 갯수가 같아야 함.
# test_list_3rd의 데이터 갯수 24개, 그러므로 24개의 갯수를 가진 어떤 형태이든 데이터를 바꿀 수 있음.
np.shape(test_list_3rd)
>>> (3, 2, 4)np.reshape(test_list_3rd, (4,6))
>>> array([[1, 2, 3, 4, 5, 6],
[7, 8, 1, 2, 3, 4],
[5, 6, 7, 8, 1, 2],
[3, 4, 5, 6, 7, 8]])
# 데이터 차원확인 np.ndim( )
# 데이터가 존재하는 축방향이 늘어나면 차원수도 늘어남
# 기하학적 데이터의 차원수를 이야기하고
# 데이터분석을 할 때는 열기준으로 차원을 이야기 한다.
np.ndim(test_list_3rd)
>>> 3
# 전치행렬 축방향을 바꾸어서 새로운 행렬 생성해준다! np.transpose( )
np.transpose(test_list_3rd)
>>> array([[[1, 1, 1],
[5, 5, 5]],
[[2, 2, 2],
[6, 6, 6]],
[[3, 3, 3],
[7, 7, 7]],
[[4, 4, 4],
[8, 8, 8]]])
7. Numpy array (배열, 행렬)
- numpy 연산의 기본이 되는 데이터 구조입니다.
- 리스트보다 간편하게 만들 수 있으며 연산이 빠른 장점이 있습니다.
- 브로드캐스팅 연산을 지원합니다.
- 단, 같은 type의 데이터만 저장 가능합니다.
- array 또한 numpy의 기본 함수로서 생성 가능합니다.
- array 함수 호출 기본구조
ex) np.array(배열변환 대상 데이터)
ex) np.arange(start, end, step_forward)
- array 함수 호출 기본구조
7.1 numpy array 실습
# 기존 데이터 구조(리스트)를 array로 변환
test_array = np.array(test_list)
test_array2 = np.array(test_list2)
test_farray = np.array(test_flist)
test_array_2nd = np.array(test_list_2nd)
test_array_3rd = np.array(test_list_3rd)
# array 생성 확인
# 리스트에서 array 형태로 들어가 있다.
test_array
>>> array([1, 2, 3, 4])
# 같은 타입의 데이터만 들어가는지 확인
np.array([1,2,3.14])
>>> array([1. , 2. , 3.14])# 전부 실수가 된다.
# 전부 문자열로 된다
# 정수-> 실수 -> 문자열로 바뀌는 거는 쉽다. 반대는 어렵다.
np.array(["100",1,2])
>>> array(['100', '1', '2'], dtype='<U11')
# 2차원 배열 확인
test_array_2nd
>>> array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
# 3차원 배열 확인
test_array_3rd
>>> array([[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[1, 2, 3, 4],
[5, 6, 7, 8]]])
# np.arange 함수로 생성
np.arange(30).reshape(2,5,3)
>>> array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11],
[12, 13, 14]],
[[15, 16, 17],
[18, 19, 20],
[21, 22, 23],
[24, 25, 26],
[27, 28, 29]]])
7.2 특수한 형태의 array를 함수로 생성
함수 호출의 기본구조
ex) np.ones([자료구조 shape])
자료구조 shape은 정수, [ ]리스트, ( ) 튜플 로만 입력가능합니다.
- ones()
- zeros()
- empty()
- eye()
# 1로 초기화한 array 생성
np.ones((5, 5))
>>> array([[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.],
[1., 1., 1., 1., 1.]])
# 0으로 초기화
np.zeros((4,4))
>>> array([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]])
# numpy.empty 함수는 (값의 초기화를 수행하지 않고) 주어진 형태와 타입을 갖는 새로운 어레이를 반환한다.
# 주의해야 할 것은 메모리도 초기화되지 않기 때문에 예상하지 못한 쓰레기 값이 들어가 있습니다.
np.empty([2,3,4])
>>> array([[[6.23042070e-307, 4.67296746e-307, 1.69121096e-306,
3.33773471e-307],
[3.44898162e-307, 2.33638188e-307, 7.56587584e-307,
1.37961302e-306],
[1.05699242e-307, 8.01097889e-307, 1.78020169e-306,
7.56601165e-307]],
[[1.02359984e-306, 1.15710088e-306, 6.23056330e-307,
1.60219578e-306],
[7.56601165e-307, 6.23061763e-307, 9.34607074e-307,
8.90098127e-307],
[8.90108313e-307, 6.23053954e-307, 1.69118515e-306,
8.34451928e-308]]])
# 항등행렬 초기화
# 항등행렬의 수학적 의미는 항등행렬 X A = A
# shape이 안맞는 경우 연산이 가능하도록 할 때
# 항등행열: 행과 열의 갯수와 같은 행렬
# 항등행열 X 행열 = 그냥 곱한 행열이 나옴
# 역도 성립
np.eye(5)
>>> array([[1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0.],
[0., 0., 0., 0., 1.]])
7.3 array 속성 및 내장함수
np.array 에는 유용한 수리, 통계 연산을 위한 함수가 갖추어져 있다.
다차원 기하학적 연산을 위한 함수도 함께 살펴보자.
array 내장 속성 호출 기본구조
ex) test_array.ndim
자주 사용하는 속성 shape, dtype, ndim
array 내장함수 호출 기본구조
ex) test_array.prod( )
7.3.1 array 속성
test_array
>>> array([1, 2, 3, 4])
# 데이터 타입확인
test_array.dtype # 속성
>>> dtype('int32')
# 원소의 항목의 데이터 타입을 보여줌, int32 32비트 정수
# test_array 클래스 안에 속해있는 dtype이라는 속성
# 데이터구조 확인, 가장많이 사용됨 np.shape()
test_array.shape
>>> (4,)
# 데이터 차원 확인
test_array.ndim
>>> 1
# 전치행렬
test_array.T
>>> array([1, 2, 3, 4, 5])
7.3.2 array 내장함수
# 내장함수 호출
# np.sum() 썼던 대로 사용하면 적용가능
# 보통 연산을 위한 함수가 많이 쓰임
# numpy 함수와 키워드가 같다.
test_array.sum()
>>> 15
7.4 array 연산
# 리스트연산 test
[1,2,3,4] + [5]
>>> [1, 2, 3, 4, 5]
a = [1, 2, 3, 4]
for item in a:
print(item + 5)
>>> 6
7
8
9
# array 덧셈, 뺄셈, 곱셈, 나눗셈
test_array + 5
>>> array([6, 7, 8, 9])
# (5, 5, 5, 5)를 더한것과 같은 결과 = 브로드 캐스팅
test_array * 5
>>> array([ 5, 10, 15, 20])
test_array > 5
>>> array([False, False, False, False])
# 참 거짓도 벡터 연산으로 표현 가능
# 실제 연산속도 차이를 확인하기 위한 큰 데이터 생성
big_list = [i for i in range(50000000)]
big_array = np.array(big_list)executed in 7.53s, finished 13:36:39 2022-07-25
# 리스트 연산테스트
big_list_1 = [i + 1 for i in big_list]
CPU times: total: 4.33 s
Wall time: 4.61 s
# array 연산테스트
big_array_1 = big_array + 1
CPU times: total: 93.8 ms
Wall time: 99.6 ms
# 브로드 캐스팅을 통해서 4.64s 에서 123ms로 엄청나게 빠르게 줄었다!
# 행렬내적
a = np.arange(24).reshape(4,6)
b = np.arange(60).reshape(6,10)
# 행렬내적 연산
# 내적연산자 @
a @ barray([[ 550, 565, 580, 595, 610, 625, 640, 655, 670, 685],
[1450, 1501, 1552, 1603, 1654, 1705, 1756, 1807, 1858, 1909],
[2350, 2437, 2524, 2611, 2698, 2785, 2872, 2959, 3046, 3133],
[3250, 3373, 3496, 3619, 3742, 3865, 3988, 4111, 4234, 4357]])
# b @ a 는 10) @ (4 이므로 안됨
7.5 벡터 가중합
벡터의 내적은 가중합을 계산할 때 쓰일 수 있습니다. 가중합(weighted sum)이란 복수의 데이터를 단순히 합하는 것이 아니라 각각의 수에 어떤 가중치 값을 곱한 후 이 곱셈 결과들을 다시 합한 것을 말한다.
데이터 벡터가 x=[x1,⋯,xN]^T이고 가중치 벡터가 w=[w1,⋯,wN]^T이면 데이터 벡터의 가중합은 다음과 같다.

쇼핑을 할 때 각 물건의 가격은 데이터 벡터, 각 물건의 수량은 가중치로 생각하여 내적을 구하면 총금액을 계산할 수 있다.
# 벡터의 가중합 연습문제
# 삼성전자, 셀트리온, 카카오로 포트폴리오를 구성하려한다.
# 각 종목의 가격은 80,000원, 270,000원, 160,000원이다.
# 삼성전자 100주, 셀트리온 30주, 카카오 50주로 구성하기 위한 매수금액을 구하시오
# (80000 * 100) + (270000 * 30) + (160000 * 50)
price = [80000, 270000,160000]
price = np.array(price)
stock = [100, 30, 50]
stock = np.array(stock)
price @ stock24100000
# 내부적으로 T 한 값을 확인을 한다. 그래서 (1,3)(1,3) 인데도 내적이 되었다.
# 선형 회귀모델 y = b1x1 + b2x2 ...... (벡터의 가중합은 선형회귀 모델(?))
8. array 인덱싱, 슬라이싱(매우중요)
기본적으로 자료구조란 데이터의 묶음, 그 묶음을 관리 할 수 있는 바구니를 이야기 한다.
데이터 분석을 위해 자료구조를 사용하지만 자료구조안 내용에 접근을 해야 할 경우도 있다.
인덱싱이란?
데이터 바구니 안에 든 내용 하나에 접근하는 명령, 인덱스는 내용의 순번
슬라이싱이란?
데이터 바구니 안에 든 내용 여러가지에 접근 하는 명령
기본적으로 인덱싱과 슬라이싱의 색인은 리스트와 동일
8.1 인덱싱, 슬라이싱 실습
import numpy as np
# 10부터 19까지 범위를 가지는 array생성
index_array = np.arange(10,20)
index_array
>>> array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19])
# 0부터 3번 인덱스까지
index_array[0:4]
>>> array([10, 11, 12, 13])
# 4번 인덱스부터 마지막 인덱스까지
index_array[4:]
>>> array([14, 15, 16, 17, 18, 19])
# 마지막 인덱스부터 뒤에서 3번째 인덱스까지
index_array[-3:]
>>> array([17, 18, 19])
# 0부터 3씩 증가하는 인덱스
index_array[range(0,10,3)]
index_array[ : : 3]
>>> array([10, 13, 16, 19])
8.2 여러가지 인덱싱 및 슬라이싱 방법을 시도해봅시다
# 인덱싱 테스트 array 생성
index_test2 = np.array(range(25)).reshape([5, 5])
index_test2array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19],
[20, 21, 22, 23, 24]])
index_test2[2 : , 1 : 4]
>>> array([[11, 12, 13],
[16, 17, 18],
[21, 22, 23]])
index_test2[ : 2, 2 : 5]
>>> array([[2, 3, 4],
[7, 8, 9]])
index_test2[ : , 1]
>>> array([ 1, 6, 11, 16, 21])
# 3차원 배열 슬라이싱
# 바깥쪽 기준으로 슬라이싱
# 그다음 안쪽 데이터를 슬라이싱 한다
index_test3 = np.arange(40).reshape(2, 5, 4)
index_test3
>>> array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15],
[16, 17, 18, 19]],
[[20, 21, 22, 23],
[24, 25, 26, 27],
[28, 29, 30, 31],
[32, 33, 34, 35],
[36, 37, 38, 39]]])
index_test3[0, 3:, 1:3]
>>> array([[13, 14],
[17, 18]])
index_test3[ :, 2: , :3]
>>> array([[[ 8, 9, 10],
[12, 13, 14],
[16, 17, 18]],
[[28, 29, 30],
[32, 33, 34],
[36, 37, 38]]])
index_test3[ :, :,1]
>>> array([[ 1, 5, 9, 13, 17],
[21, 25, 29, 33, 37]])
9. 팬시인덱싱
# 테스트 array 생성
pet = np.array(['개', '고양이', '고양이', '햄스터', '개', '햄스터'])
num = np.array([1, 2, 3, 4, 5, 6])
indexing_test = np.arange(30).reshape(6,5)
indexing_test
>>> array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19],
[20, 21, 22, 23, 24],
[25, 26, 27, 28, 29]])
# num array 조건연산
num > 4 # 여기도 브로드 캐스팅 적용!
>>> array([False, False, False, False, True, True])
num == 4
>>> array([False, False, False, True, False, False])
# 팬시인덱스
# True False 로 적힌 것을 인덱스로 사용하겠다.
indexing_test[pet == "고양이"] # array([False, True, True, False, False, False])를 전달한것
# 인덱스 중에 1, 2 에 해당하는 행을 뽑아냄array([[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
indexing_test[num == 4 ] # array([False, False, False, True, False, False])를 전달한것array([[15, 16, 17, 18, 19]])
# 조건연산 추가 sum, any, all
# 어떤 데이터가 어떤 방식으로 있는지 간단하게 검증할 수 있다.
(pet == "고양이").sum() # 판다스에서 True 1 False 0
# 고양이 2개 인 데이터가 2개 있음
>>> 2
(pet == "고양이").any() # 값이 고양이인 데이터가 하나라도 있으면 참
>>> True
(pet == "고양이").all() # 데이터가 모두 고양이여야 True
>>> False'Python > Data Analysis Library' 카테고리의 다른 글
| Pandas_ex (연습문제) (0) | 2022.07.27 |
|---|---|
| 02. Package pandas finance (0) | 2022.07.27 |
| Part03 Chapter.02 데이터 분석 라이브러리 09. seaborn plots (실습) (0) | 2022.07.24 |
| Part03 Chapter.02 데이터 분석 라이브러리 08 pyplot 기초 (실습) (0) | 2022.07.24 |
| Part03 Chapter.02 데이터 분석 라이브러리 07. Seaborn을 사용하는 이유 (0) | 2022.07.18 |



